使用 Newton-Raphson method 求平方根

前言

牛顿-拉弗森方法(Newton-Raphson method)，是一种在实数域和复数域上近似求解方程的方法，基本思想是利用函数的切线来找到更接近根的值。

假设在$[a,b]$上连续单调的函数$f(x)$，求方程$f(x)=0$的近似解。

详细步骤

1. 选择一个初始值

选择一个最接近函数$f(x)$零点的$x_0$，这个值最好接近实际根。

2. 迭代

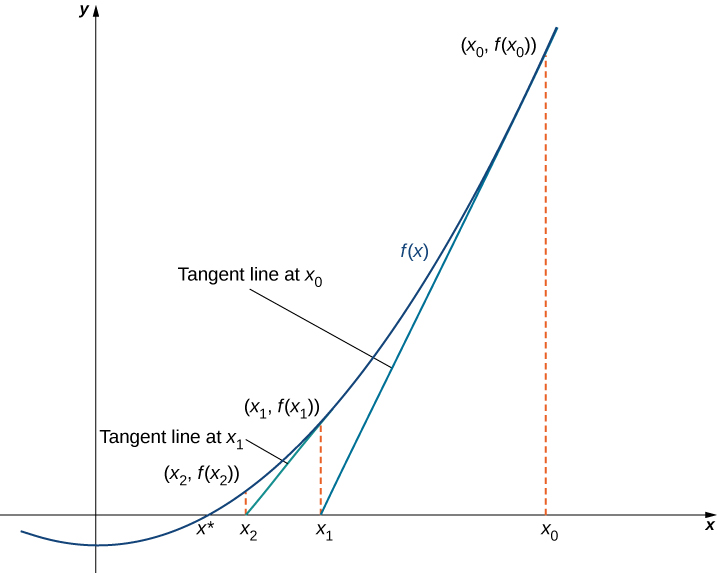
在$x=x_0$处，计算$f(x_0)$以及导数值$f’(x_0)$。之后计算函数$f(x)$在$x=x_0$处的切线与$x$轴的交点。

切线计算方程：
$$
y - f(x_0) = f’(x_0)(x-x_0)
$$
设$x=x_0$处切线与$x$轴的交点为$x_1$，则$x_1$计算：
$$
\displaylines {0 - f(x_0) = f’(x_0)(x_1-x_0) \
x_1=x_0-\frac{f(x_0)}{f’(x_0)}}
$$
继续求$x=x_1$处的切线与$x$轴的交点$x_2$，不断迭代逼近零点，根据上式得出迭代公式：
$$
x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}
$$

3. 收敛判定

重复步骤 2，直到满足收敛条件，如$\left | x_{n+1} \right | - \left | x_n \right | < ϵ$

牛顿法通常具有二次收敛性，意味着每次迭代的误差大约会平方，前提是初始猜测足够接近实际根且导数不为零。

注意事项

初始猜测的选择至关重要，若选择不当，可能导致发散或收敛到错误的根。
当导数为零或接近零时，方法可能失效。
应用时需确保函数在所选区间内是连续且可导的。

LeetCode 应用

69.Sqrt(x)

69.Sqrt(x)可以使用牛顿法，此题目要求给出一个数，求其平方根。

分析问题

我们要计算一个非负整数 x 的平方根，目标是找到一个非负数 y，使得：
$$
y^2-x=0
$$
在这里，我们定义一个函数：
$$
f(y)=y^2-x
$$
求$f(y)=0$的解。

牛顿法步骤

根据以上的迭代公式，求出$y_{n+1}$：
$$
y_{n+1}=y_n-\frac{y^2_n-x}{2y_n}=y_n+\frac{x-y^2_n}{2y_n}=\frac{y_n+\frac{x}{y_n}}{2}
$$

代码实现

class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0:
            return 0
        # 初始值
        guess = x
        while guess * guess > x:
            # 开始迭代
            guess = (guess + x // guess) // 2
        return guess

367. Valid Perfect Square

367. Valid Perfect Square与上题思想类似，递推公式也一样。

代码实现

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        if num == 1:
            return True
        
        x = num
        while x * x > num:
            x = (x + num // x) // 2
        
        return x * x == num

后记

牛顿法比二分法效率要高