抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

LeetCode-Hot100-二分查找

leetcode

发布于：2024年11月15日

字数：3.7k 字

时长：17 分钟

前言

题单LeetCode 热题 100的二分查找部分，给出解析。

35. Search Insert Position

原题链接

题目描述

Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You must write an algorithm with O(log n) runtime complexity.

Example 1: 

1
2
Input: nums = [1,3,5,6], target = 5
Output: 2

Example 2: 

1
2
Input: nums = [1,3,5,6], target = 2
Output: 1

Example 3: 

1
2
Input: nums = [1,3,5,6], target = 7
Output: 4

Constraints:

  • 1 <= nums.length <= 10^4
  • -10^4 <= nums[i] <= 10^4
  • nums contains distinct values sorted in ascending order.
  • -10^4 <= target <= 10^4

解题方法

排序数组找目标值，优先考虑二分查找。

初始化两个指针，一个指针指向头部，一个指针指向尾部，每一次判断两个指针中间的值，比目标值大则调整尾指针，比目标值小则调整头指针。

代码实现

1
2
3
4
5
6
7
8
9
10
class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        low, high = 0, len(nums) - 1
        while low <= high:
            mid = (low + high) // 2
            if nums[mid] < target:
                low = mid + 1
            else:
                high = mid - 1
        return low

复杂度分析

时间复杂度：$O(logn)$

空间复杂度：$O(1)$

74. Search a 2D Matrix

原题链接

题目描述

You are given an m x n integer matrix matrix with the following two properties:

  • Each row is sorted in non-decreasing order.
  • The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1: 

1
2
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2: 

1
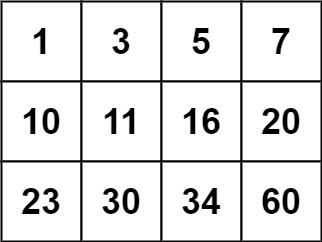
2
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • -10^4 <= matrix[i][j], target <= 10^4

解题方法

这个问题可以通过二分查找来高效解决。由于矩阵每一行都是按非严格递增排列，并且每一行的第一个元素大于前一行的最后一个元素，可以把整个矩阵看成一个有序的数组。通过在这个一维有序数组中进行二分查找，就能有效地找到目标值。

思路：

  1. 将矩阵看成一个一维有序数组，通过二分查找来查找目标元素。
  2. 将矩阵的下标转换为一维数组的下标。假设矩阵的大小是 m x n，那么位置 (i, j) 对应一维数组中的索引为 i * n + j。
  3. 利用二分查找来判断目标值是否存在。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix:
            return False

        m, n = len(matrix), len(matrix[0])
        left, right = 0, m * n - 1  # 一维数组的左右边界

        while left <= right:
            mid = (left + right) // 2
            mid_value = matrix[mid // n][mid % n]  # 获取对应的二维矩阵元素

            if mid_value == target:
                return True
            elif mid_value < target:
                left = mid + 1
            else:
                right = mid - 1

        return False

复杂度分析

时间复杂度：$O(log(m×n))$

空间复杂度：$O(1)$

34. Find First and Last Position of Element in Sorted Array

原题链接

题目描述

Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.

If target is not found in the array, return [-1, -1].

You must write an algorithm with O(log n) runtime complexity.

Example 1: 

1
2
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]

Example 2: 

1
2
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]

Example 3: 

1
2
Input: nums = [], target = 0
Output: [-1,-1]

Constraints:

  • 0 <= nums.length <= 10^5
  • -10^9 <= nums[i] <= 10^9
  • nums is a non-decreasing array.
  • -10^9 <= target <= 10^9

解题方法

要在有序数组中找到指定值 target 的起始和结束位置，并保证算法的时间复杂度为 $O(log n)$，可以使用二分查找（Binary Search）的方法。

思路如下：

  • 二分查找左边界：通过二分查找找到 target 第一次出现的位置。
  • 二分查找右边界：通过二分查找找到 target 最后一次出现的位置。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def findLeft(nums, target):
    left, right = 0, len(nums) - 1

    while left <= right:
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return left

def findRight(nums, target):
    left, right = 0, len(nums) - 1

    while left <= right:
        mid = (left + right) // 2
        if nums[mid] <= target:
            left = mid + 1
        else:
            right = mid - 1
    return right

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        left = findLeft(nums, target)
        right = findRight(nums, target)

        if left <= right and nums[left] == target and left <= len(nums):
            return [left, right]
        return [-1, -1]

findLeft 函数：

  • 目标：找到 target 在数组中第一次出现的位置，即左边界。

  • 过程：

    1. 初始化两个指针，left 指向数组的起始位置，right 指向数组的末尾。
    2. 进入一个 while 循环，条件是 left <= right，表示当搜索区间还存在时继续执行。
    3. 计算 mid，即中间位置的索引：mid = (left + right) // 2。
    4. 判断
      • 如果 nums[mid] < target：说明 target 在 mid 右边，因此移动 left 指针到 mid + 1，排除左半部分。
      • 否则，说明 target 可能在 mid 处或者左边，因此移动 right 指针到 mid - 1，缩小搜索范围。
    5. 循环结束时，left 指向的是第一个大于等于 target 的元素位置。

findRight 函数：

  • 目标：找到 target 在数组中最后一次出现的位置，即右边界。

  • 过程：

    1. 与 findLeft 类似，初始化 left 和 right 指针。
    2. 进入 while 循环，条件是 left <= right。
    3. 计算 mid 的位置：mid = (left + right) // 2。
    4. 判断
      • 如果 nums[mid] <= target：说明 target 可能在 mid 处或者右边，因此移动 left 指针到 mid + 1，排除左半部分。
      • 否则，target 在 mid 左边，因此移动 right 指针到 mid - 1。
    5. 循环结束时，right 指向的是最后一个小于等于 target 的元素位置。

总结：

  • findLeft 函数的作用是找到 target 的左边界，它通过不断缩小搜索区间，最终返回第一个 >= target 的位置。
  • findRight 函数的作用是找到 target 的右边界，它通过类似的方法，最终返回最后一个 <= target 的位置。

复杂度分析

时间复杂度：$O(logn)$

空间复杂度：$O(1)$

33. Search in Rotated Sorted Array

原题链接

题目描述

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] ( 0-indexed ). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

Example 1: 

1
2
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2: 

1
2
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Example 3: 

1
2
Input: nums = [1], target = 0
Output: -1

Constraints:

  • 1 <= nums.length <= 5000
  • -10^4 <= nums[i] <= 10^4
  • All values of nums are unique .
  • nums is an ascending array that is possibly rotated.
  • -10^4 <= target <= 10^4

解题方法

这个问题是一个典型的「旋转排序数组」查找问题。我们需要在一个旋转过的有序数组中使用二分查找方法查找目标值，时间复杂度要求是 $O(log n)$。为了实现这一点，我们可以利用旋转数组的特性，通过判断数组的左右部分是否有序来缩小查找范围。

思路：

  1. 数组被旋转后，数组的一部分是有序的，另一部分也是有序的。我们可以利用这个性质进行二分查找。
  2. 在每次二分查找时，判断中间元素和左右端点的关系：
    • 如果左半部分有序，判断目标值是否在左半部分的范围内。
    • 如果右半部分有序，判断目标值是否在右半部分的范围内。

通过这种方式，我们可以在 $O(log n)$ 时间内找到目标值。

算法步骤：

  1. 初始化两个指针，left 和 right，分别指向数组的左右两端。
  2. 进入循环，当 left 小于等于 right 时：
    • 计算中间位置 mid = (left + right) // 2。
    • 如果 nums[mid] == target，返回 mid。
    • 如果左半部分有序，即 nums[left] <= nums[mid]：
      • 如果 target 在左半部分范围内，即 nums[left] <= target < nums[mid]，则将 right = mid - 1，否则将 left = mid + 1。
    • 如果右半部分有序，即 nums[mid] <= nums[right]：
      • 如果 target 在右半部分范围内，即 nums[mid] < target <= nums[right]，则将 left = mid + 1，否则将 right = mid - 1。
  3. 如果循环结束后仍然没有找到目标，返回 -1。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        while left <= right:
            mid = (left + right) // 2
            
            if nums[mid] == target:
                return mid
            
            # 判断左半部分是否有序
            if nums[left] <= nums[mid]:
                if nums[left] <= target < nums[mid]:
                    right = mid - 1  # target在左半部分
                else:
                    left = mid + 1  # target在右半部分
            # 判断右半部分是否有序
            else:
                if nums[mid] < target <= nums[right]:
                    left = mid + 1  # target在右半部分
                else:
                    right = mid - 1  # target在左半部分
        
        return -1  # 找不到target

复杂度分析

时间复杂度：$O(logn)$

空间复杂度：$O(1)$

153. Find Minimum in Rotated Sorted Array

原题链接

题目描述

Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:

  • [4,5,6,7,0,1,2] if it was rotated 4 times.
  • [0,1,2,4,5,6,7] if it was rotated 7 times.

Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].

Given the sorted rotated array nums of unique elements, return the minimum element of this array.

You must write an algorithm that runs in O(log n) time.

Example 1: 

1
2
3
Input: nums = [3,4,5,1,2]
Output: 1
Explanation: The original array was [1,2,3,4,5] rotated 3 times.

Example 2: 

1
2
3
Input: nums = [4,5,6,7,0,1,2]
Output: 0
Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times.

Example 3: 

1
2
3
Input: nums = [11,13,15,17]
Output: 11
Explanation: The original array was [11,13,15,17] and it was rotated 4 times.

Constraints:

  • n == nums.length
  • 1 <= n <= 5000
  • -5000 <= nums[i] <= 5000
  • All the integers of nums are unique .
  • nums is sorted and rotated between 1 and n times.

解题方法

这道题的目的是在一个经过旋转的升序数组中找到最小元素，且要求时间复杂度为 $O(log n)$。我们可以使用 二分查找来解决这个问题，因为旋转后的数组依然保持着部分有序的性质。

思路：

  1. 给定一个数组 nums，它是一个升序数组经过旋转后的结果。数组的最小值就是旋转点所在的位置。
  2. 旋转后的数组将会分为两个部分：一部分是升序的，另一部分也是升序的。旋转后，数组的最小值总是在两个部分的交界处。
  3. 利用二分查找，可以根据当前中间元素与数组的左右边界元素的大小关系来判断最小值的所在区间。

算法步骤：

  • 设定两个指针 left 和 right，分别指向数组的开始和结束。
  • 计算中间元素 mid = (left + right) // 2。
  • 如果中间元素大于右边的元素 nums[mid] > nums[right]，说明最小值在 mid 右边，此时 left = mid + 1。
  • 如果中间元素小于等于右边的元素 nums[mid] <= nums[right]，说明最小值在 mid 左边或就是 mid 本身，此时 right = mid。
  • 循环直到 left 等于 right，此时 nums[left] 就是最小元素。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def findMin(self, nums: List[int]) -> int:
        left, right = 0, len(nums) - 1
        
        while left < right:
            mid = (left + right) // 2
            
            # 如果中间值大于右边值，说明最小值在右边
            if nums[mid] > nums[right]:
                left = mid + 1
            else:
                right = mid  # 中间值可能就是最小值，因此 right 赋值为 mid
        
        return nums[left]

复杂度分析

时间复杂度：$O(log n)$，因为每次二分查找将搜索区间缩小一半。

空间复杂度：$O(1)$，只使用了常数级别的额外空间。

4. Median of Two Sorted Arrays

原题链接

题目描述

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be O(log (m+n)).

Example 1: 

1
2
3
Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.

Example 2: 

1
2
3
Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Constraints:

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000
  • -10^6 <= nums1[i], nums2[i] <= 10^6

解题方法

这个问题要求我们在两个已排序的数组中找到中位数，并且要在 $O(log(m+n))$ 的时间复杂度内完成。我们可以利用二分查找的思想来解决。

解决思路：

假设我们有两个已排序的数组 nums1 和 nums2，我们需要在它们的合并数组中找到中位数。直接合并两个数组并排序的时间复杂度是 $O((m+n) log(m+n))$，这显然不满足题目对时间复杂度的要求。因此，我们可以利用二分查找来优化这一过程。

我们可以通过在较小的数组上进行二分查找，来逐步缩小问题的规模。具体步骤如下：

  1. 保证数组 nums1 更小：如果 nums1 比 nums2 大，我们交换它们，以确保我们总是在较小的数组上进行二分查找。

  2. 二分查找：在 nums1 上进行二分查找，设定一个切分点 i，然后根据 i 的位置计算 nums2 中的切分点 j，使得左右两部分元素的数量相等或尽量接近。

  3. 判断是否找到合适的切分点：

    • 确保左半部分的最大值小于右半部分的最小值，即：
      • nums1[i-1] <= nums2[j] 和 nums2[j-1] <= nums1[i]。
    • 如果不满足条件，调整二分查找的范围。

  4. 计算中位数：

    • 如果两个数组的总长度是奇数，中位数是左半部分的最大值。
    • 如果是偶数，中位数是左右两部分最大值和最小值的平均。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        # 确保 nums1 是较小的数组
        if len(nums1) > len(nums2):
            nums1, nums2 = nums2, nums1

        m, n = len(nums1), len(nums2)
        left, right = 0, m

        while left <= right:
            i = (left + right) // 2  # nums1 的切分点
            j = (m + n + 1) // 2 - i  # nums2 的切分点

            # 边界处理
            maxLeft1 = float('-inf') if i == 0 else nums1[i - 1]
            minRight1 = float('inf') if i == m else nums1[i]
            
            maxLeft2 = float('-inf') if j == 0 else nums2[j - 1]
            minRight2 = float('inf') if j == n else nums2[j]

            # 满足条件
            if maxLeft1 <= minRight2 and maxLeft2 <= minRight1:
                if (m + n) % 2 == 1:
                    return max(maxLeft1, maxLeft2)  # 奇数长度，中位数为左半部分的最大值
                else:
                    return (max(maxLeft1, maxLeft2) + min(minRight1, minRight2)) / 2  # 偶数长度，中位数为两部分的平均值
            elif maxLeft1 > minRight2:
                right = i - 1  # 减小 i
            else:
                left = i + 1  # 增大 i

复杂度分析

时间复杂度：$O(log(min(m, n)))$，由于我们在较小的数组上进行二分查找，最坏情况下的时间复杂度是 $O(log(min(m, n)))$。

空间复杂度：$O(1)$，只使用了常数级别的额外空间。

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://blog.skyheart.moe/posts/972954ad/

更新于：2024年11月18日

二分查找

评论