循环不变量(Loop invariant)——概念介绍

前言

经常在一些算法大牛们的算法题解中看到「循环不变量」这个概念，初次看到时不明就里，然而这似乎又是一个很重要的概念，不能够蒙混过去，于是在查阅了部分资料后得作此文，权当抛砖引玉。

概述

循环不变量是在循环的每次迭代之前和迭代之后都必然为「真」的条件（迭代过程中的「真」或「假」此处没有提及）。

举例，在 Python 中，一个 While 循环满足如下形式，其中 B 是一个布尔表达式（我们称其为循环的守护条件）并且 S 是一系列命令/指令（我们称其为循环的主体）。

1
2

while B:
    S

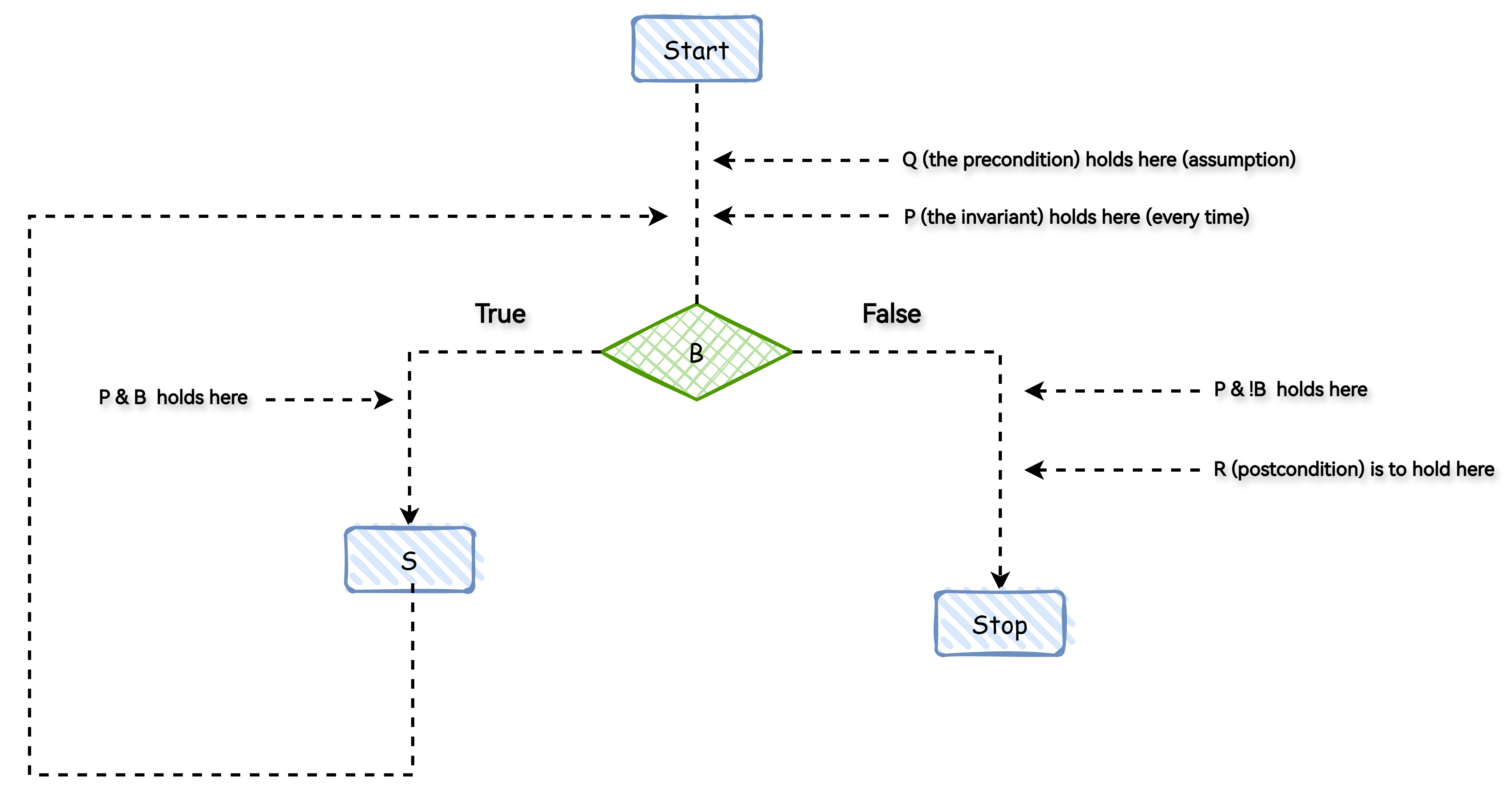
此类循环执行的流程图如下：

假设 B 不会更改程序中变量的值。

介绍这个流程图中循环执行的逻辑结构，具体步骤：

1. 开始节点：流程从 start 节点开始。
2. **前置条件 Q**：在开始时，假设前置条件 Q 成立，允许进入后续步骤。
3. 循环判断：从 Q 节点进入判断，如果不变式 P成立且布尔条件 B 成立，执行步骤 S。这个过程意味着在每次循环开始时，不变式 P 保持不变。
4. 布尔条件判断：如果 B 为真，流程继续执行步骤 S；如果 B 为假，流程将跳出循环，进入停止节点。
5. **结束条件 R**：在停止节点之前，确保后置条件 R 成立，表示循环已经正确执行并达到预期结果。

假设每次执行到流程图中的「关键位置」（即表示条件 B 的菱形框上方的位置）时 P 总是成立。选择一个作为循环不变式的 P 很容易，即在关键位置总是成立的 P。（例如，选择 P 为 true 就可以。）然而，选择一个在证明 R 成立时有用的 P 并不总是容易。为了有用，所选择的不变式 P 应满足以下条件：

1

P & !B ==> R

即 P 和循环守护条件 B 的否定同时为真时，R 也为真。为什么？因为这样我们可以确保，当循环结束时（此时 P & !B 必然成立），R 也会像我们期望的那样成立。

循环不变量如何保证「不变」？

你可能会好奇：如何保证你选择的 P 每次执行到关键位置时确实为真？

我们通过如下步骤进行分析：

首先，需要证明 Q ==> P，即前置条件 Q 的真实性能够保证不变式 P 为真。由此可以得出，执行第一次到达关键位置时，P 是成立的。

其次，需要证明每次后续执行到关键位置时，P 依然成立。为此，需要证明：如果在一个 P & B 成立的状态下开始执行 S（循环体），那么在 S 执行完毕时，P 必然仍然为真。（当然，这相当于证明 {P & B} S {P} 是一个有效的 Hoare triple。）

实际上，这相当于对循环迭代次数进行数学归纳法证明。第一步是基准情形，证明在执行第一次到达关键位置时（即在零次迭代之后），P 是成立的。第二步是归纳步骤，证明：如果对于任意正整数 n，P 在第 n 次执行到关键位置时成立（即在第 n-1 次迭代后），那么它在第 n+1 次（即第 n 次迭代后）也必须成立。

循环不变量如何保证循环「终止」？

要证明循环在有限次迭代后终止，我们需要表明每次迭代都在某种程度上向终止推进。技术上，这意味着要证明存在一个程序变量的整数函数 *g*，该函数：

1. 在每次迭代中减少；
2. 并且该函数的值必须大于零，才能进行下一次迭代（换句话说，P&B 的真实性保证该函数的值大于零）。

请注意，在每次循环迭代的开始，该函数的值是剩余要执行的迭代次数的上限。

例如，考虑以下循环：

1
2

while i < n: 
    i = i + 1 

在这里，我们可以将 g 定义为 n-i，可以看到每次迭代时 g 的值都会减少（因为 i 每次增加而 n 保持不变）。同时，循环守护条件 i < n 的真实性保证了 g 的值大于零，这是我们所需要的。

为了说明循环不变式概念的实用性，我们可以讨论一些有趣的小问题。

例子

红蓝混合的弹珠罐

假设存在一个装有一个或多个弹珠的罐子，每个弹珠的颜色是红色或者蓝色。你有不限量的红色弹珠可以使用，执行以下过程：

1
2
3
4
5
6
7
8

while 罐子里的弹珠数 > 1:
    从罐子里选择任意两个弹珠
    if 这两个弹珠颜色相同:
        把它们扔掉
      	放入一个红色弹珠到罐子里
   	else:   # 选中了一个红色和一个蓝色的弹珠
      	把选中的红色弹珠扔掉
      	将选中的蓝色弹珠放回罐子

通过模拟这个过程，你可以很容易地验证，每次循环迭代后，罐子里的弹珠数都会减少正好一个。因此，如果罐子最初包含 N 个弹珠，那么经过 N-1 次循环迭代后，罐子里恰好会剩下一个弹珠。我们刚刚通过一个有说服力但非正式的论证表明，这个循环在有限次迭代后会终止。为了更加精确，我们可以显式定义 g 为一个函数，该函数应用于罐子中的弹珠时，返回罐子里弹珠的数量。然后，我们可以论证，每次循环迭代时，*g* 的值都会减少，此外，如果循环条件成立（即罐子里至少有两个弹珠），*g* 的值一定大于零。

假设我们知道罐子里最初有多少红色和蓝色弹珠。拥有这些信息后，我们是否能够确定地预测罐子里最后剩下的弹珠是什么颜色？（请注意，由于我们假设罐子最初不为空且每次迭代弹珠的数量都会减少一个，因此不可能最终得到一个空罐子。）

更正式地说：

是否存在一个函数f: N × N --> {BLUE, RED}（即 f 的定义域是自然数对的集合，值域是集合 {BLUE, RED}），它满足以下条件：

对于所有 K 和 M（其中至少有一个非零），如果我们从罐子里开始有 K 个红色弹珠和 M个蓝色弹珠，那么罐子里最后剩下的弹珠的颜色一定是 f(K,M)？

事实证明，这样的函数存在！关键在于首先识别与罐子里蓝色弹珠数量有关的循环不变量。

考虑一次循环迭代对罐子里蓝色弹珠数量的影响。如果选中的两个弹珠颜色相同，那么蓝色弹珠的数量要么减少两个（如果两个都是蓝色弹珠），要么保持不变（如果两个都是红色弹珠）。如果选中的两个弹珠颜色不同，蓝色弹珠的数量保持不变。

由此可以得出，单次循环迭代不会影响罐子里蓝色弹珠数量的奇偶性（即，罐子里蓝色弹珠的数量要么保持奇数，要么保持偶数）。同样地，这一特性适用于循环的任意次数的迭代。设 M 和 m 分别表示罐子里蓝色弹珠最初和当前的数量，则有：

当且仅当 M 是奇数时，m 也是奇数

这是循环的一个不变量。如果你觉得更容易理解，这一循环不变量也可以表达为：

（M 和 m 都是奇数）或（M 和 m 都是偶数）

假设最初罐子里的蓝色弹珠数量 M 是奇数，并且循环刚刚终止。（请记住，由于循环不变量在每次迭代结束时都成立，因此它特别在最后一次迭代结束时成立。）那么，罐子里剩下的唯一弹珠必须是蓝色的，因为否则我们会有 m = 0，这是偶数。同理，我们可以得出，如果 M 是偶数，那么剩下的弹珠一定是红色的，因为否则我们会有 m = 1，这是奇数。

因此，上述函数 f 如下：

1
2

f(K,M) = { RED   当M为偶数时
         { BLUE  否则（即M为奇数时）

有趣的是，最后剩下的弹珠的颜色完全不依赖于罐子里最初的红色弹珠数量。

后记