LeetCode-Hot100-矩阵

前言

题单LeetCode 热题 100的矩阵部分，给出解析。

73. Set Matrix Zeroes

题目描述

Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0‘s.

You must do it in place.

Example 1:

1 2	Input: matrix = [[1,1,1],[1,0,1],[1,1,1]] Output: [[1,0,1],[0,0,0],[1,0,1]]

Example 2:

1 2	Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]

Constraints:

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2^31 <= matrix[i][j] <= 2^31 - 1

Follow up:

A straightforward solution using O(mn) space is probably a bad idea.
A simple improvement uses O(m + n) space, but still not the best solution.
Could you devise a constant space solution?

解题方法

该题要求我们把出现 0 的行与列的元素全都设置为 0，通用的思路是遍历整个矩阵找到出现 0 的位置，则时间复杂度必定为 $O(m×n)$，那么如何减少空间复杂度呢？

思路一：使用 O(m+n) 额外存储空间

第一遍遍历整个 matrix，第一遍用集合记录有哪些行、列出现 0；第二遍遍历置 0。

思路二：使用 O(1) 存储空间

使用 matrix 本身的行列来记录该行该列是否有 0，当做标记位。

如果对应行列出现了 0，则其第一行与第一列的位置必然也是 0

考虑用 matrix 第一行和第一列记录该行与该列是否有 0，但同时也要对第一行第一列本身设置一个标志位，防止自己这一行（一列）也出现 0。

代码实现

思路一：

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        m, n = len(matrix), len(matrix[0])
        rows = [False] * m  # 记录哪些行需要置0
        cols = [False] * n  # 记录哪些列需要置0

        # 第一遍遍历矩阵，标记需要置0的行和列
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == 0:
                    rows[i] = True
                    cols[j] = True

        # 第二遍遍历矩阵，根据标记将相应的行和列置0
        for i in range(m):
            for j in range(n):
                if rows[i] or cols[j]:
                    matrix[i][j] = 0

思路二：

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        m, n = len(matrix), len(matrix[0])
        
        # 标记第一行和第一列是否包含0
        first_row_has_zero = any(matrix[0][j] == 0 for j in range(n))
        first_col_has_zero = any(matrix[i][0] == 0 for i in range(m))

        # 使用第一行和第一列来标记需要置0的行和列
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] == 0:
                    matrix[i][0] = 0  # 标记这一行
                    matrix[0][j] = 0  # 标记这一列

        # 根据标记将对应的行和列置0
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0

        # 根据first_row_has_zero标记处理第一行
        if first_row_has_zero:
            for j in range(n):
                matrix[0][j] = 0

        # 根据first_col_has_zero标记处理第一列
        if first_col_has_zero:
            for i in range(m):
                matrix[i][0] = 0

复杂度分析

时间复杂度：$O(m×n)$

空间复杂度：$O(1)$

54. Spiral Matrix

原题链接

题目描述

Given an m x n matrix, return all elements of the matrix in spiral order.

Example 1:

1 2	Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [1,2,3,6,9,8,7,4,5]

Example 2:

1 2	Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

解题方法

模拟螺旋的过程即可。

从左到右遍历，如果左边界超出右边界则跳出，抵达右边界时，上边界下移。
从上到下遍历，如果上边界超出下边界则跳出，抵达下边界时，右边界左移。
从右到左遍历，如果左边界超出右边界则跳出，抵达左边界时，下边界上移。
从下到上遍历，如果上边界超出下边界则跳出，抵达上边界时，左边界右移。

代码实现

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        result = []
        if not matrix:
            return []
        
        top, bottom, left, right = 0, len(matrix)-1, 0, len(matrix[0])-1

        while True:
            # 从左到右，如果左边界超出右边界则跳出
            if left > right: break
            for i in range(left, right+1):
                result.append(matrix[top][i])
            top += 1
            
            # 从上到下，如果上边界超出下边界则跳出
            if top > bottom: break
            for i in range(top, bottom+1):
                result.append(matrix[i][right])
            right -= 1

            # 从右到左，如果左边界超出右边界则跳出
            if left > right: break
            for i in range(right, left-1, -1):
                result.append(matrix[bottom][i])
            bottom -= 1

            # 从下到上，如果上边界超出下边界则跳出
            if top > bottom: break
            for i in range(bottom, top-1, -1):
                result.append(matrix[i][left])
            left += 1


        return result

复杂度分析

时间复杂度：$O(m×n)$，m == matrix.length, n == matrix[i].length

空间复杂度：$O(1)$

48. Rotate Image

原题链接

题目描述

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place , which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

1 2	Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

1 2	Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Constraints:

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

解题方法

本题要求对整个矩阵进行顺时针 90° 的翻转，通过观察旋转前后元素的位置，可以得到原本在 matrix[i][j] 位置上的元素被转移到 matrix[j][n-i-1] 上。考虑将这个转换过程分解。

先将原来的数组进行转置，即行列关系对调，使得 matrix[i][j] 与 matrix[j][i] 互换。这一操作相当于将矩阵沿主对角线（从左上到右下的对角线翻转）。

例如对于矩阵：

转置完成之后，将每一行的元素从左到右进行反转，从而达到顺时针 90° 旋转的效果。

对于上面的转置矩阵：

完成顺时针 90° 旋转的效果。

代码实现

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix)
    
        # 1. 先转置矩阵
        for i in range(n):
            for j in range(i, n):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        
        # 2. 手动翻转每一行
        for i in range(n):
            for j in range(n // 2):
                matrix[i][j], matrix[i][n - j - 1] = matrix[i][n - j - 1], matrix[i][j]

复杂度分析

时间复杂度：$O(n^2)$

空间复杂度：$O(1)$

240. Search a 2D Matrix II

原题链接

题目描述

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

Integers in each row are sorted in ascending from left to right.
Integers in each column are sorted in ascending from top to bottom.

Example 1:

1 2	Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true

Example 2:

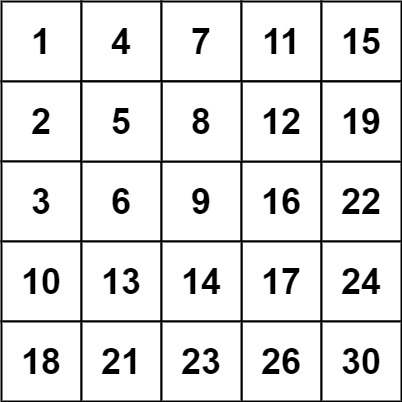
1 2	Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false

Constraints:

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-10^9 <= matrix[i][j] <= 10^9
All the integers in each row are sorted in ascending order.
All the integers in each column are sorted in ascending order.
-10^9 <= target <= 10^9

解题方法

需要查找矩阵中的一个目标值，先分析矩阵的特性：

矩阵每行的元素从左到右升序排列。
矩阵每列的元素从上到下升序排列。

根据以上两条特性，可以得出：矩阵最右上方的值是其对应行的最大值，对应列的最小值。

那么每次查找时，只需要和矩阵最右上方的值进行比较。如果目标值小于矩阵最右上方的值，则目标值可能在左部分的行中，继续查询左边一行的值；如果目标值大于矩阵最右上方的值，则目标值可能在下部分的列中，继续查询下边一列的值。

步骤如下：

初始化一个指针指向矩阵的右上角（row = 0，col = n - 1）。
进入循环，直到指针超出矩阵边界：
- 如果当前元素等于目标值，返回 true。
- 如果当前元素小于目标值，移动指针向下（row++）。
- 如果当前元素大于目标值，移动指针向左（col--）。
如果循环结束仍未找到目标值，返回 false。

代码实现

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        row, col = 0, n - 1
        
        while row < m and col >= 0:
            if matrix[row][col] == target:
                return True
            elif matrix[row][col] < target:
                row += 1
            else:
                col -= 1
                
        return False

复杂度分析

时间复杂度：$O(m+n)$

空间复杂度：$O(1)$