LeetCode-Hot100-链表

前言

题单LeetCode 热题 100的链表部分，给出解析。

160. Intersection of Two Linked Lists

题目描述

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1:

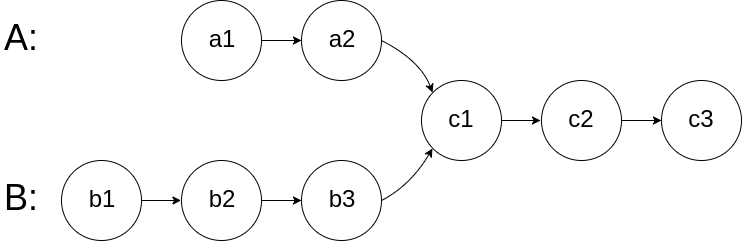
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Custom Judge:

The inputs to the judge are given as follows (your program is not given these inputs):

intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.
listA - The first linked list.
listB - The second linked list.
skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.

The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted .

Example 1:

Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory.

Example 2:

Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:

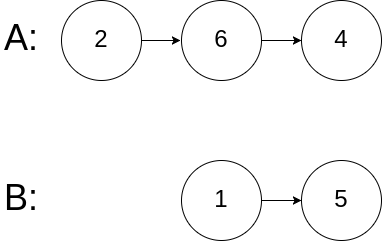
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

Constraints:

The number of nodes of listA is in the m.
The number of nodes of listB is in the n.
1 <= m, n <= 3 * 10^4
1 <= Node.val <= 10^5
0 <= skipA < m
0 <= skipB < n
intersectVal is 0 if listA and listB do not intersect.
intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

Follow up: Could you write a solution that runs in O(m + n) time and use only O(1) memory?

解题方法

题目要求我们找出两个链表可能存在的相交节点，并将其返回。

需要明确的是，两个链表的相交节点一定是「相同」的节点，即判断一个节点是否是相交节点，直接将两个链表上的节点进行对比判断是否相同即可。

哈希表

思路是遍历第一个链表，将所有节点存储到一个哈希表中，然后遍历第二个链表，检查其节点是否在哈希表中。如果存在就返回对应的节点，不存在则遍历完成之后返回 NULL。

栈

创建两个栈，分别将两个链表中的所有节点分别压入两个栈中。栈顶节点与链表尾节点相对应。

同时从两个栈中弹出节点，比较它们是否相同。重复这一过程直到找到最后一个相同的节点，这个节点就是链表的相交节点。

如果两个链表在某一处相交，则从相交部分到尾部的长度是一样的，节点是相同的。

如果栈中的节点不再相同或一个栈为空时，之前的那个相同节点就是两个链表相交的节点。如果所有节点都不同，说明链表不相交，返回 NULL。

双指针

双指针有两种做法，一种是「重置指针」，一种是「尾部对齐」。

重置指针思想：

初始化两个指针 ptrA 与 ptrB，分别指向两个链表 headA 与 headB 的头结点。

使用这两个指针同时遍历链表。如果 ptrA 到达链表 A 的末尾，则将它重置到链表 B 的开头。同样，如果 ptrB 到达链表 B 的末尾，则将它重置到链表 A 的开头。

继续这一过程，直到 ptrA 和 ptrB 指向同一个节点，也就是相交节点，或者直到两个指针都到达末尾（都变为 null），表明没有交点。

重置指针的思想在于，切换链表之后，指针会走过相同的距离，当它们在相交节点相遇时会对齐。（相当于另类的两表拼接，消除二表之间的长度差，如果相交会有共同的尾部，不相交则指向 NULL）。

尾部对齐思想：

先计算两个链表的长度，让较长的链表先走其与较短链表的长度差步，再同时遍历两个链表，直到出现相交节点或为空。

让较长链表先走的目的是让其剩余部分到尾部的距离和较短链表是一样的，从相交部分到尾部的长度对于两个链表也是一样长的。

代码实现

哈希表

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
        nodes_in_A = set()

        # 遍历链表 A，存储所有节点到哈希集合中
        while headA:
            nodes_in_A.add(headA)
            headA = headA.next

        # 遍历链表 B，检查是否有节点在哈希集合中
        while headB:
            if headB in nodes_in_A:
                return headB
            headB = headB.next

        return None

栈

  def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:

      # 创建两个栈
      stackA, stackB = [], []
      
# 将链表A的所有节点压入栈
      while headA:
          stackA.append(headA)
          headA = headA.next

      # 将链表B的所有节点压入栈
      while headB:
          stackB.append(headB)
          headB = headB.next

      # 初始化交点为None
      intersection_node = None
      
      # 同时弹出两个栈的节点并比较它们
      while stackA and stackB:
          topA = stackA.pop()
          topB = stackB.pop()

          # 如果节点相同，说明这是一个可能的相交节点
          if topA == topB:
              intersection_node = topA
          else:
              break

      # 返回最后一个相同的节点，或者None（如果没有相交）
      return intersection_node

双指针

重置指针：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
        if not headA or not headB:
            return None
        
        # 两个指针初始化为各自链表的头节点
        ptrA, ptrB = headA, headB
        
        # 遍历两个链表
        while ptrA != ptrB:
            # 如果指针到达链表末尾，则重置到另一个链表的头节点
            if ptrA is not None:
                ptrA = ptrA.next
            else:
                ptrA = headB

            if ptrB is not None:
                ptrB = ptrB.next
            else:
                ptrB = headA
        
        # 如果两个指针相遇，返回相交节点；否则返回None
        return ptrA

尾部对齐：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

  

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
        # 统计A,B表长
        len1, len2 = 0,0
        # 移动指针到两个表的表尾，统计表长
        moveA, moveB = headA, headB

        while moveA:
            len1 += 1
            moveA = moveA.next

        while moveB:
            len2 += 1
            moveB = moveB.next

        # 长表尾部对齐短表
        if len1 < len2:
            for _ in range(len2 - len1):
                headB = headB.next
        else:
            for _ in range(len1 - len2):
                headA = headA.next

        while headA and headB and headA != headB:
            headA = headA.next
            headB = headB.next

        # 如果相交，返回相交点
        return headA

复杂度分析

方法	时间复杂度	空间复杂度
哈希表	$O(m+n)$（两表总长）	$O(m)$ 或 $O(n)$
栈	$O(m+n)$（两表总长）	$O(m+n)$
双指针	$O(m+n)$（两表总长）	$O(1)$

206. Reverse Linked List

原题链接

题目描述

Given the head of a singly linked list, reverse the list, and return the reversed list.

Example 1:

1 2	Input: head = [1,2,3,4,5] Output: [5,4,3,2,1]

Example 2:

1 2	Input: head = [1,2] Output: [2,1]

Example 3:

1 2	Input: head = [] Output: []

Constraints:

The number of nodes in the list is the range [0, 5000].
-5000 <= Node.val <= 5000

Follow up: A linked list can be reversed either iteratively or recursively. Could you implement both?

解题方法

给出一个单链表的头节点 head，将整个链表进行反转。根据这个要求，给出两种做法。

迭代（双指针）

从头节点开始，定义两个指针，cur 指向当前节点（需要反转的那个节点），pre 指向前一个节点（当前节点反转之后的下一个节点）。

从头节点开始，头节点反转之后变成尾节点，所以初始化 pre=NULL，cur=head。同时需要保证链表不断链，要用一个额外变量存储当前节点的下一个节点。

算法步骤：

定义 pre=NULL 与 cur=head。
进入循环，当 cur==NULL 时跳出循环。
定义变量 next_node 暂存 cur 的下一个节点，用于后续遍历。
将 cur 的 next 指针指向 pre，实现反转。
将 pre 移动到 cur 的位置，准备下次迭代。
将 cur 移动到下一个节点 next_node，继续循环。

递归

持续递归遍历直到最后一个节点，从最深的递归层开始反转。

举例：现有一个链表1 -> 2 -> 3 -> 4 -> 5 -> None

步骤 1：初始调用 reverseList(1)

1 2	调用栈: reverseList(1) 链表状态: 1 -> 2 -> 3 -> 4 -> 5 -> None

此时链表的头节点是 1，将调用 reverseList(2)。

步骤 2：递归调用 reverseList(2)

1 2	调用栈: reverseList(1) -> reverseList(2) 链表状态: 1 -> 2 -> 3 -> 4 -> 5 -> None

此时链表的头节点是 2，将调用 reverseList(3)。

步骤 3：递归调用 reverseList(3)

1 2	调用栈: reverseList(1) -> reverseList(2) -> reverseList(3) 链表状态: 1 -> 2 -> 3 -> 4 -> 5 -> None

此时链表的头节点是 3，将调用 reverseList(4)。

步骤 4：递归调用 reverseList(4)

1 2	调用栈: reverseList(1) -> reverseList(2) -> reverseList(3) -> reverseList(4) 链表状态: 1 -> 2 -> 3 -> 4 -> 5 -> None

此时链表的头节点是 4，将调用 reverseList(5)。

步骤 5：递归调用 reverseList(5)

1 2	调用栈: reverseList(1) -> reverseList(2) -> reverseList(3) -> reverseList(4) -> reverseList(5) 链表状态: 1 -> 2 -> 3 -> 4 -> 5 -> None

此时链表的头节点是 5，因为 5 的 next 是 None，返回节点 5。

步骤 6：从最深递归层开始反转

1 2	调用栈: reverseList(1) -> reverseList(2) -> reverseList(3) -> reverseList(4) 链表状态: 5 -> 4 -> 3 -> 2 -> 1 -> None

在每个返回的递归层中，逐步反转节点的next指向。

4.next.next = 4，即让5指向4，然后4.next = None，链表变为：5 -> 4 -> None
3.next.next = 3，即让4指向3，然后3.next = None，链表变为：5 -> 4 -> 3 -> None
2.next.next = 2，即让3指向2，然后2.next = None，链表变为：5 -> 4 -> 3 -> 2 -> None
1.next.next = 1，即让2指向1，然后1.next = None，链表变为：5 -> 4 -> 3 -> 2 -> 1 -> None

最终，整个链表被反转。

代码实现

迭代（双指针）

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
		prev = None  # prev 指针用于指向前一个节点，初始为 None
		current = head  # current 指针用于遍历链表，初始指向链表头节点  
        
        while current is not None:  # 当 current 不为 None 时，继续循环  
		    next_node = current.next  # 暂存 current 的下一个节点，用于后续遍历  
		    current.next = prev  # 将 current 的 next 指针指向 prev，实现反转  
		    prev = current  # 将 prev 移动到 current 的位置，准备下次迭代  
		    current = next_node  # 将 current 移动到下一个节点，继续循环  
            
        return prev  # 返回 prev 作为新链表的头节点，因为此时 current 已经是 None

递归

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # 递归终止条件：如果当前节点为空，或者下一个节点为空，直接返回当前节点
        if not head or not head.next:
            return head

        # 递归反转剩余的链表
        new_head = self.reverseList(head.next)
        # 反转当前节点与下一个节点的指向
        head.next.next = head
        head.next = None

        # 返回反转后的新头节点
        return new_head

复杂度分析

方法	时间复杂度	空间复杂度
迭代（双指针）	$O(n)$	$O(1)$
递归	$O(n)$	$O(n)$（递归调用栈）

234. Palindrome Linked List

原题链接

题目描述

Given the head of a singly linked list, return true if it is a palindrome or false otherwise.

Example 1:

1 2	Input: head = [1,2,2,1] Output: true

Example 2:

1 2	Input: head = [1,2] Output: false

Constraints:

The number of nodes in the list is in the range [1, 10^5].
0 <= Node.val <= 9

Follow up: Could you do it in O(n) time and O(1) space?

解题方法

此题要求我们检查一个链表是否为回文链表，回文链表的定义是前读与后读的结果是相同的一个序列。

此题包含了多种对链表的操作：获取链表的第 k 个节点，反转链表，链表遍历。

步骤如下：

找到链表的中间节点：使用快慢指针法，慢指针每次移动一步，快指针每次移动两步，直到快指针到达链表末尾，慢指针位于链表的中间位置。
反转链表的后半部分：从中间节点开始反转链表的后半部分。
比较前半部分和反转后的后半部分：逐一比较两部分的节点值，如果都相同则返回 True，否则返回 False。

代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def isPalindrome(self, head: Optional[ListNode]) -> bool:
        if not head or not head.next:
            return True

        # Step 1: 使用快慢指针找到中间节点
        slow, fast = head, head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next

        # Step 2: 反转链表后半部分
        prev = None
        while slow:
            next_node = slow.next
            slow.next = prev
            prev = slow
            slow = next_node

        # Step 3: 比较前半部分和反转后的后半部分
        left, right = head, prev
        while right:
            if left.val != right.val:
                return False
            left = left.next
            right = right.next

        return True

复杂度分析

时间复杂度：$O(n)$，$n$ 为链表的长度。

空间复杂度：$O(1)$，没有使用额外空间。

141. Linked List Cycle

原题链接

题目描述

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter .

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

1
2
3

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

1
2
3

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

1
2
3

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10^4].
-10^5 <= Node.val <= 10^5
pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

解题方法

本题要求判断一个链表中是否有环，就是判断在遍历过程中是否会出现「相同」的节点，可以使用双指针与哈希表两种方法。

双指针

此处使用到一个特殊的算法：Floyd's Tortoise and Hare Algorithm，又称为「龟兔赛跑算法」。

Floyd’s Tortoise and Hare 算法（Floyd’s Cycle-Finding Algorithm）是一个用来检测链表中是否存在环的经典算法。它通过使用两个不同速度的指针来遍历链表，如果链表中存在环，这两个指针最终会相遇；如果不存在环，快指针会先到达链表的末尾。

算法经典思想：

一根慢指针（乌龟）slow，每次移动一步。
一根快指针（兔子）fast，每次移动两步。
循环检测：
如果链表中存在环，快指针和慢指针最终会在环内相遇，因为快指针每次比慢指针多走一步。
如果链表中不存在环，快指针会先到达链表末尾（None），不会与快指针相遇。

哈希表

遍历所有节点，每次遍历到一个节点时，判断这个节点此前是否被访问过。

用哈希表将每个节点的引用存储到哈希表中，在遍历过程中，如果遇到某个节点已经存在于哈希表中，则说明链表存在环，因为我们又访问到了之前访问过的节点。

如果遍历完整个链表都没有遇到重复的节点，则链表中没有环。

代码实现

双指针

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        slow = head
        fast = head
        while fast is not None and fast.next is not None:
            slow = slow.next
            fast = fast.next.next

            if fast == slow:
                return True

        return False

哈希表

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        visited = set()
        cur = head

        while cur:
            if cur in visited:
                return True
            visited.add(cur)
            cur = cur.next

        return False

复杂度分析

方法	时间复杂度	空间复杂度
双指针	$O(n)$	$O(1)$
哈希表	$O(n)$	$O(n)$

142. Linked List Cycle II

原题链接

题目描述

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to ( 0-indexed ). It is -1 if there is no cycle. Note that pos is not passed as a parameter .

Do not modify the linked list.

Example 1:

1
2
3

Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

1
2
3

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

1
2
3

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10^4].
-10^5 <= Node.val <= 10^5
pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

解题方法

思路同上 141 双指针部分，不多介绍。

代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if not head or not head.next:
            return None

        slow = fast = head

        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next

            if slow == fast:
                slow = head
                while slow != fast:
                    slow = slow.next
                    fast = fast.next
                return slow

        return None

复杂度分析

时间复杂度：$O(n)$，$n$ 为链表的长度。

空间复杂度：$O(1)$，没有使用额外空间。

21. Merge Two Sorted Lists

原题链接

题目描述

You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

Example 1:

1 2	Input: list1 = [1,2,4], list2 = [1,3,4] Output: [1,1,2,3,4,4]

Example 2:

1 2	Input: list1 = [], list2 = [] Output: []

Example 3:

1 2	Input: list1 = [], list2 = [0] Output: [0]

Constraints:

The number of nodes in both lists is in the range [0, 50].
-100 <= Node.val <= 100
Both list1 and list2 are sorted in non-decreasing order.

解题方法

此问题要求我们将两个已经排序的链表合成一个新的有序链表，新的链表应该通过拼接两个链表中的节点构建。

双指针

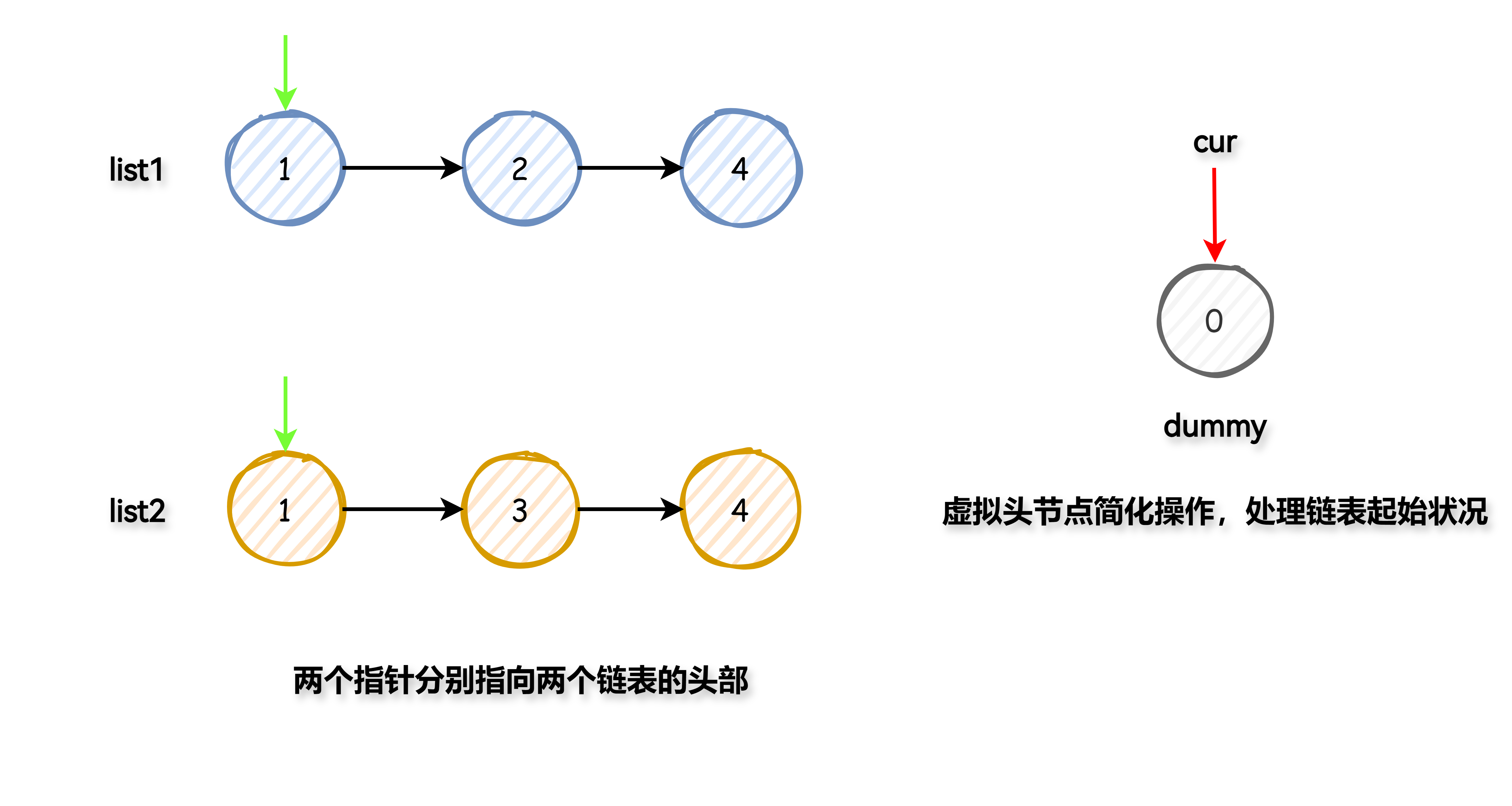
使用一个虚拟头节点简化操作，此节点并不是最终链表的一部分，只是帮忙处理链表起始情况。

将两个指针分别指向 list1 和 list2 的头部。然后，比较这两个节点的值，将较小的节点连接到新的链表上，同时移动对应的指针到下一个节点。

重复这个过程直到其中一个链表遍历完毕。

如果还有未遍历完成的链表，直接将其剩余部分连接到新链表的尾部。

返回新链表的头节点（虚拟头节点的下一个节点）。

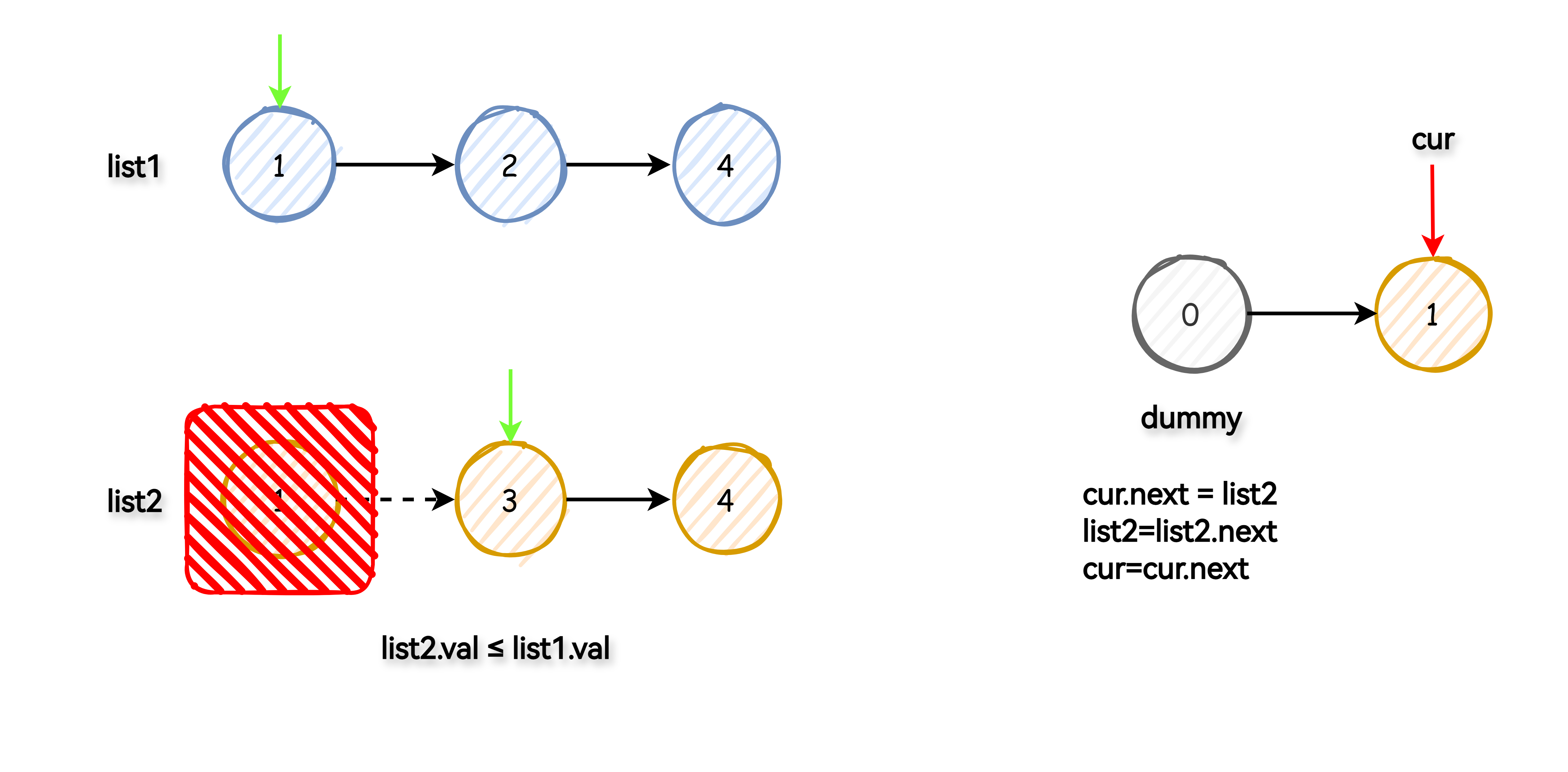
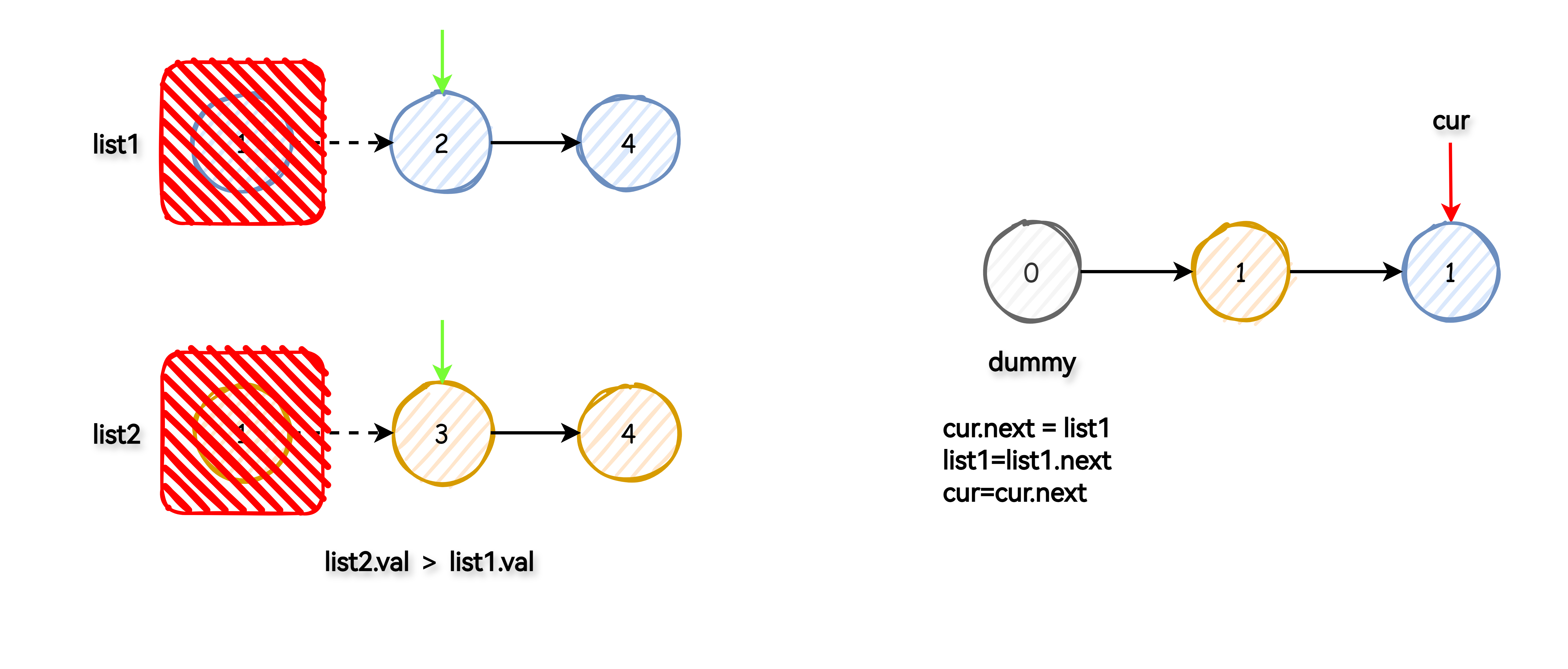
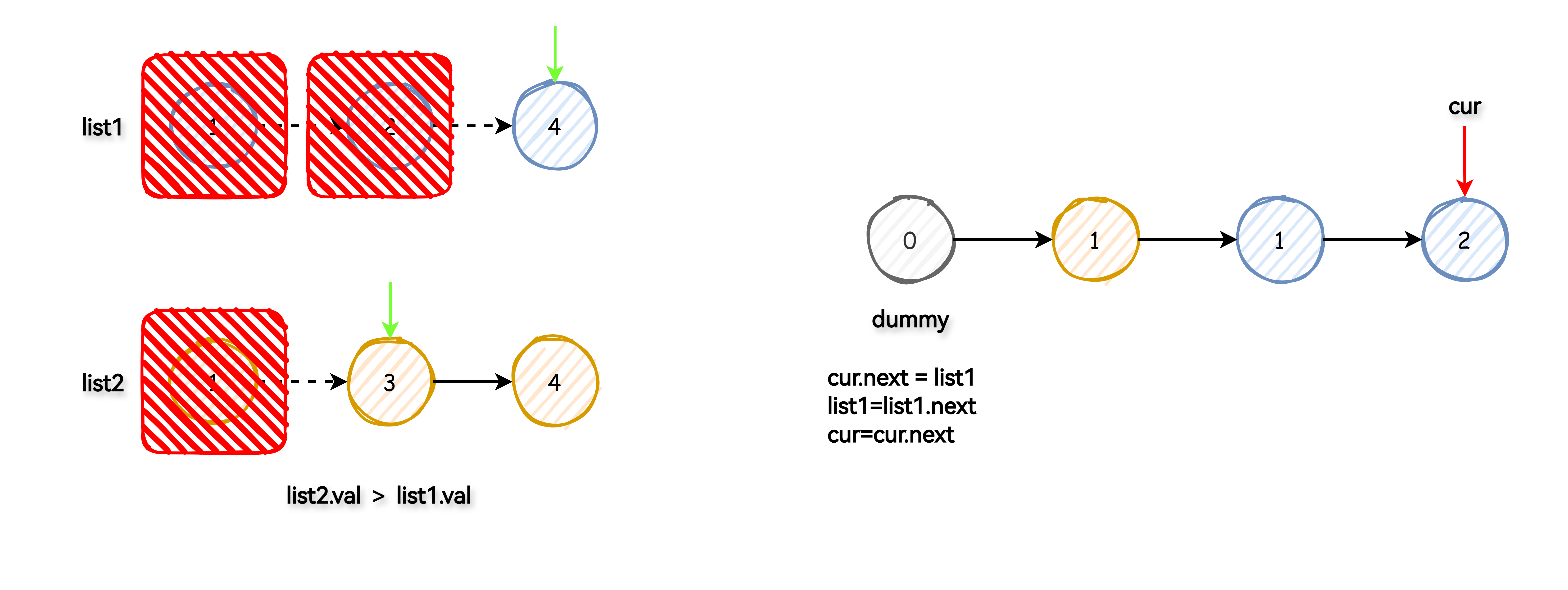
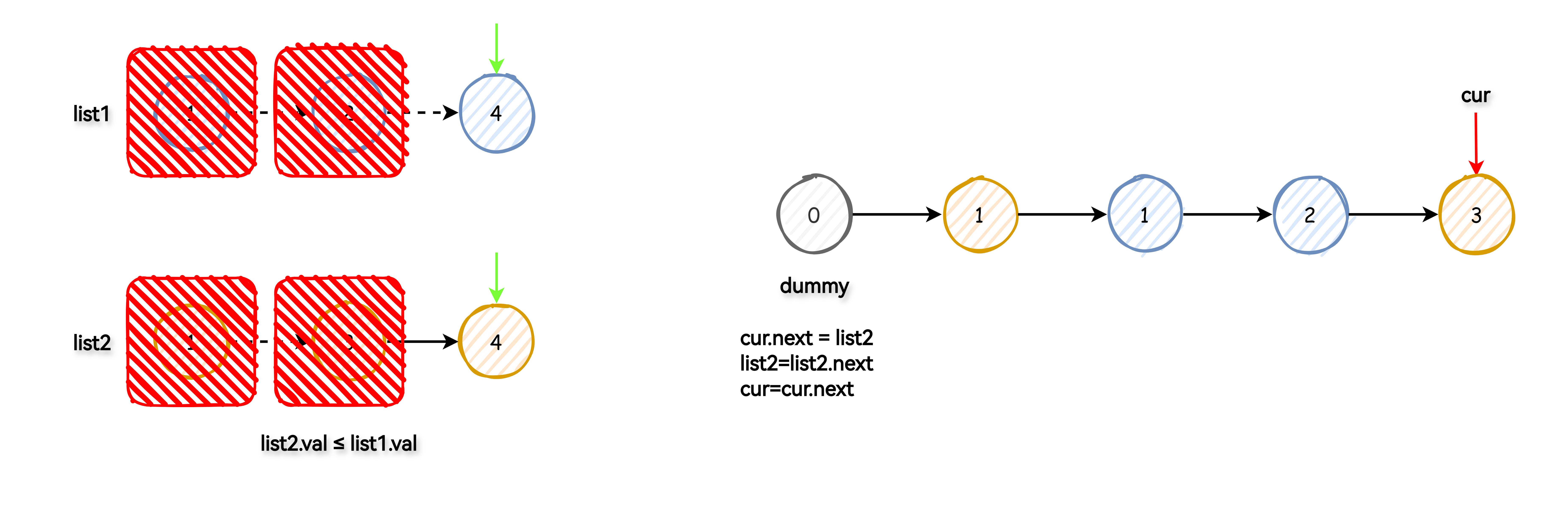
递归

递归终止条件：
- 如果 list1 为空，直接返回 list2。
- 如果 list2 为空，直接返回 list1。
递归步骤：
- 比较 list1 与 list2 当前节点的值。
- 如果 list1 的节点值较小，则将 list1 的 next 指针指向合并后的剩余部分（递归调用）。
- 如果 list2 的节点值较小或相等，则将 list2 的 next 指针指向合并后的剩余部分（递归调用）。
返回值：
- 最终返回已经合并排序好的链表的头节点

代码实现

双指针

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        # 虚拟头节点，初始化为任意值
        dummy = ListNode(0)
        current = dummy
        # 遍历两个链表
        while list1 and list2:
            if list1.val < list2.val:
                current.next = list1
                list1 = list1.next
            else:
                current.next = list2
                list2 = list2.next
            current = current.next
        # 拼接剩余部分
        current.next = list1 if list1 else list2
        # 返回头节点的后继部分
        return dummy.next

递归

# Definition for singly-linked list. 
# class ListNode: 
# 	def __init__(self, val=0, next=None): 
# 		self.val = val 
# 		self.next = next 
class Solution: 
	def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]: 
		if list1 is None: 
			return list2 
		elif list2 is None: 
			return list1 
		elif list1.val < list2.val: 
			list1.next = self.mergeTwoLists(list1.next, list2) 
			return list1 
		else: 
			list2.next = self.mergeTwoLists(list1, list2.next) 
			return list2

复杂度分析

方法	时间复杂度	空间复杂度
双指针	$O(n)$	$O(1)$
递归	$O(n)$	$O(n)$（递归调用栈的深度）

2. Add Two Numbers

原题链接

题目描述

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order , and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Example 1:

1
2
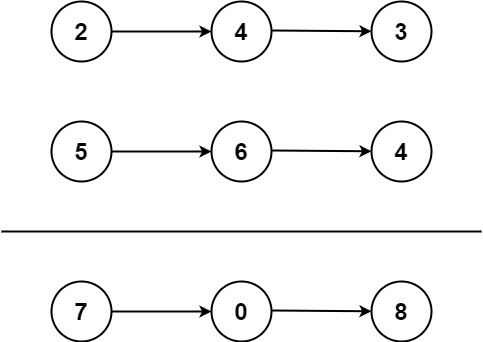
3

Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [7,0,8]
Explanation: 342 + 465 = 807.

Example 2:

1 2	Input: l1 = [0], l2 = [0] Output: [0]

Example 3:

1 2	Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] Output: [8,9,9,9,0,0,0,1]

Constraints:

The number of nodes in each linked list is in the range [1, 100].
0 <= Node.val <= 9
It is guaranteed that the list represents a number that does not have leading zeros.

解题方法

本题要求将两个链表对应节点的值加和，返回一个新的表示加和的链表，链表的值是逆序的，需要考虑进位。

迭代

初始化一个哑节点：创建一个哑节点 dummy 用于简化结果链表的操作，用 current 指针来跟踪返回链表中当前的节点。

从头遍历两个链表，计算两个链表中相对应节点的值，再加上之前结果可能出现的进位。

如果两个数相加大于或等于 10，则将进位变量 carry 标记为 1，current 的值为减 10 后的余数。

每完成一次计算，在结果链表中新加一个节点，值为计算结果。

完成两个链表的遍历之后，如果有剩余进位，则新建一个节点存储进位值。

返回哑节点的下一个结点。

递归

递归解法需要在函数中传递进位，递归的思路是，每次处理当前两链表的结点值，计算总和并得到当前结点的值与进位，然后递归处理下一个节点。

步骤：

递归基准：当两个链表都遍历完时，检查是否还有进位，如果有，则创建一个新节点存储进位。
计算当前节点的值与进位相加得到当前总和，并更新进位。递归处理下一个节点。
将计算好的结果返回。

代码实现

迭代

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
        # 初始化哑节点，进位值
        dummy = ListNode()
        current = dummy
        carry = 0

        # 循环在还有可计算的值的情况下进行
        while l1 or l2 or carry:
            # 有可能链表走到头，需要条件判断
            val1 = l1.val if l1 else 0
            val2 = l2.val if l2 else 0

            # 求和，计算进位，添加节点
            total_sum = val1 + val2 + carry
            carry = total_sum // 10
            current.next = ListNode(total_sum % 10)

            # 后移
            current = current.next
            if l1: l1 = l1.next 
            if l2: l2 = l2.next
        
        return dummy.next

递归

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode], carry = 0) -> Optional[ListNode]:
        # 基准: 如果两个链表都为空且没有进位，则结束递归
        if not l1 and not l2 and carry == 0:
            return None
        
        # 当前结点的总和
        val1 = l1.val if l1 else 0
        val2 = l2.val if l2 else 0
        total_sum = val1 + val2 + carry
        
        # 计算新的进位值
        carry = total_sum // 10
        
        # 用当前计算结果创建新的节点
        current = ListNode(total_sum % 10)
        
        # 递归处理剩余节点
        l1 = l1.next if l1 else None
        l2 = l2.next if l2 else None
        current.next = self.addTwoNumbers(l1, l2, carry)
        
        return current

复杂度分析

方法	时间复杂度	空间复杂度
迭代	$O(n)$	$O(1)$
递归	$O(n)$	$O(n)$（递归调用栈深度）

19. Remove Nth Node From End of List

原题链接

题目描述

Given the head of a linked list, remove the n^th node from the end of the list and return its head.

Example 1:

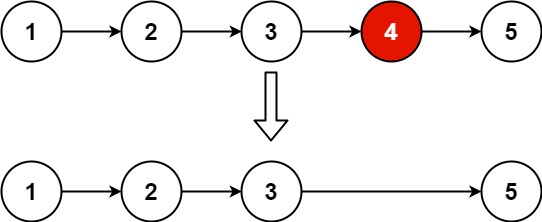
1 2	Input: head = [1,2,3,4,5], n = 2 Output: [1,2,3,5]

Example 2:

1 2	Input: head = [1], n = 1 Output: []

Example 3:

1 2	Input: head = [1,2], n = 1 Output: [1]

Constraints:

The number of nodes in the list is sz.
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

Follow up: Could you do this in one pass?

解题方法

本题要求删除倒数第 n 个链表节点，考虑使用双指针解法。

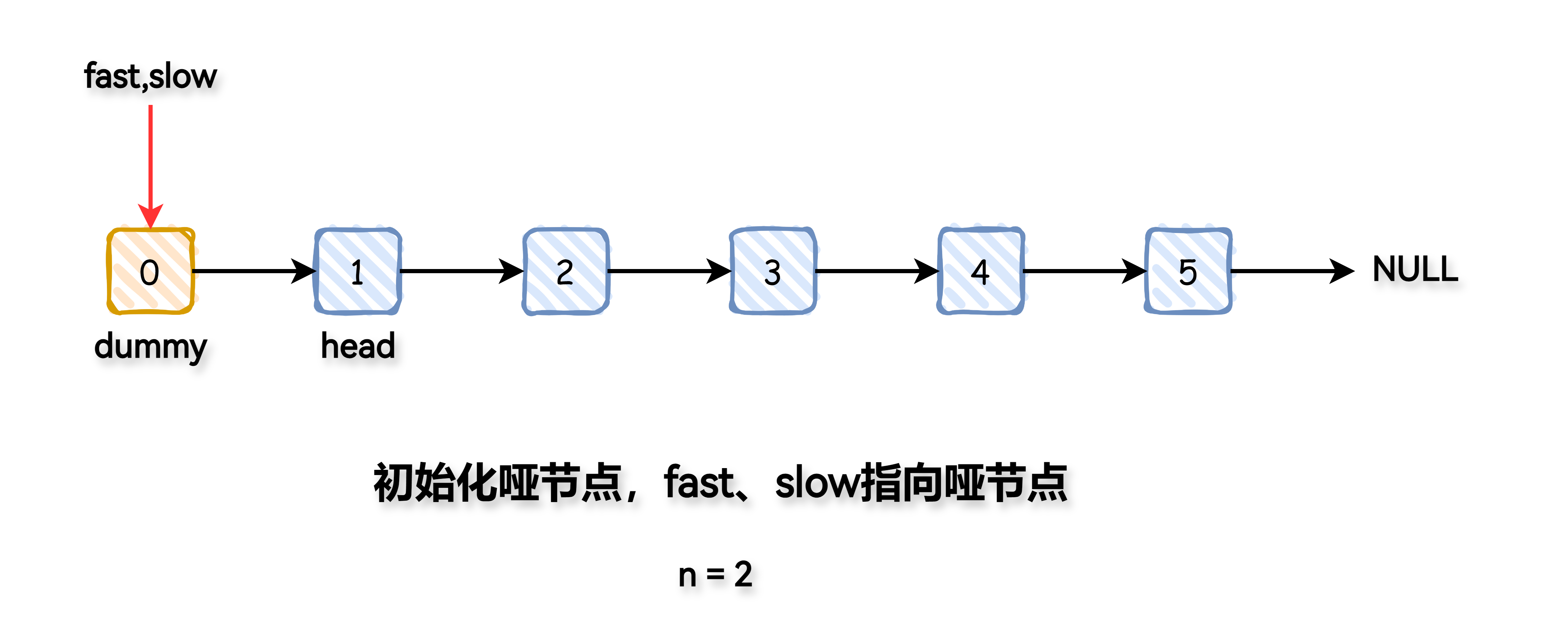
首先初始化一个哑节点 dummy，指向链表的头节点 head，使得即使删除头节点，链表操作也能够简化。

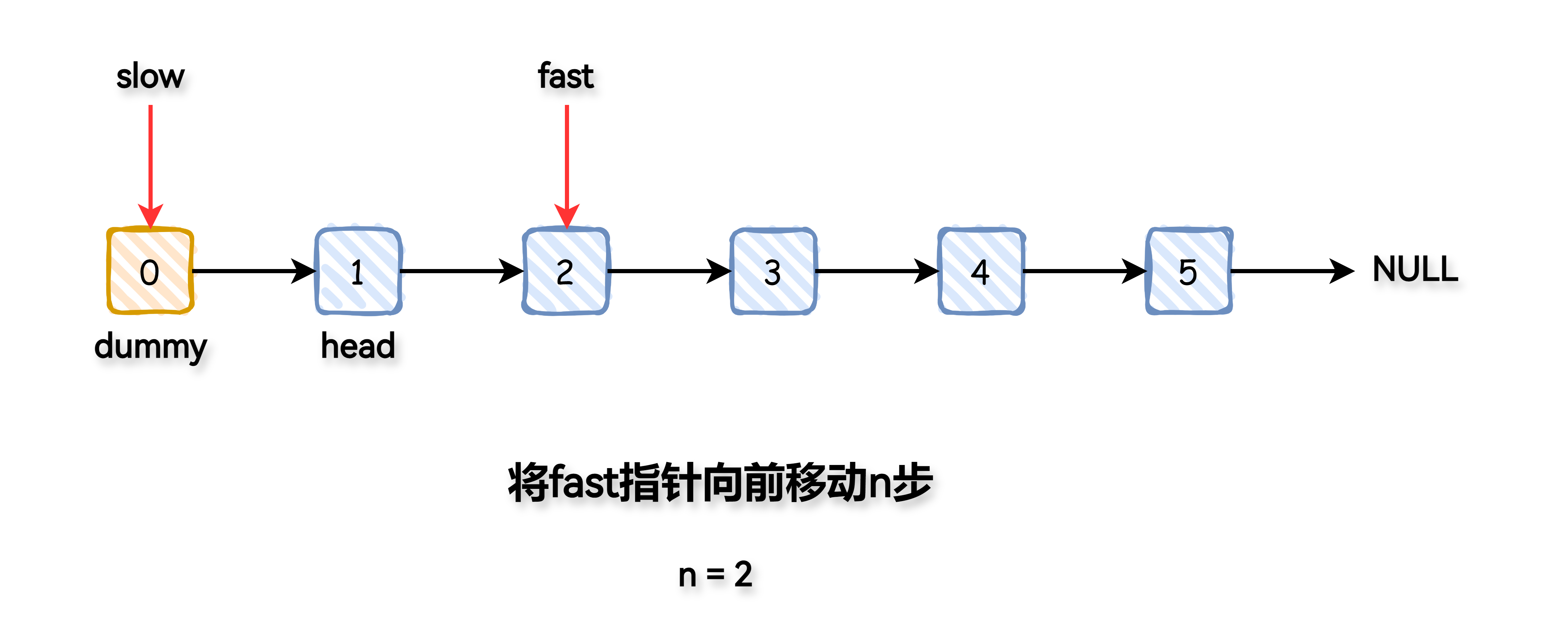
设置两个指针 fast 与 slow，都初始化为 dummy。

将 fast 指针向前先移动 n 步，使得 fast 与 slow 之间的距离为 n。

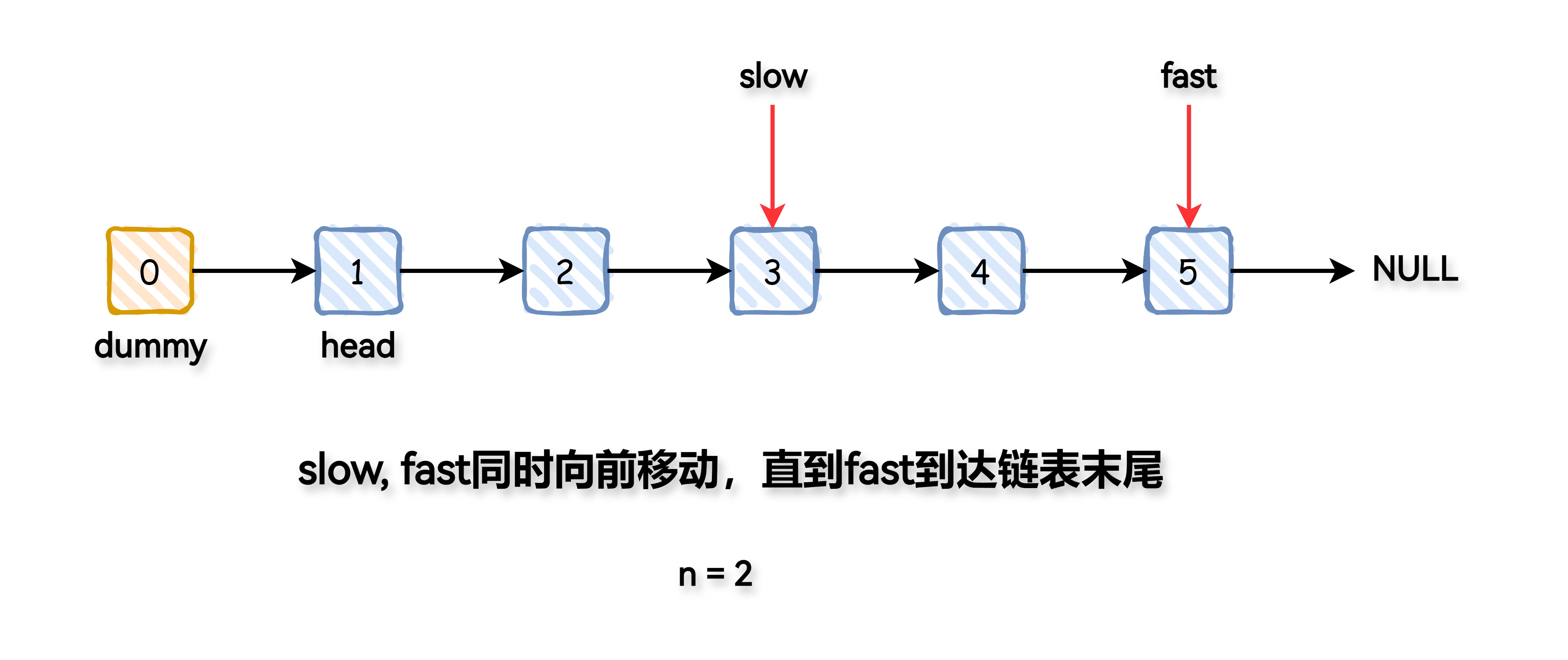
同时移动 fast 指针与 slow 指针，直到 fast 指针指向链表的末尾，此时 slow 指针指向要删除节点的前一个节点。

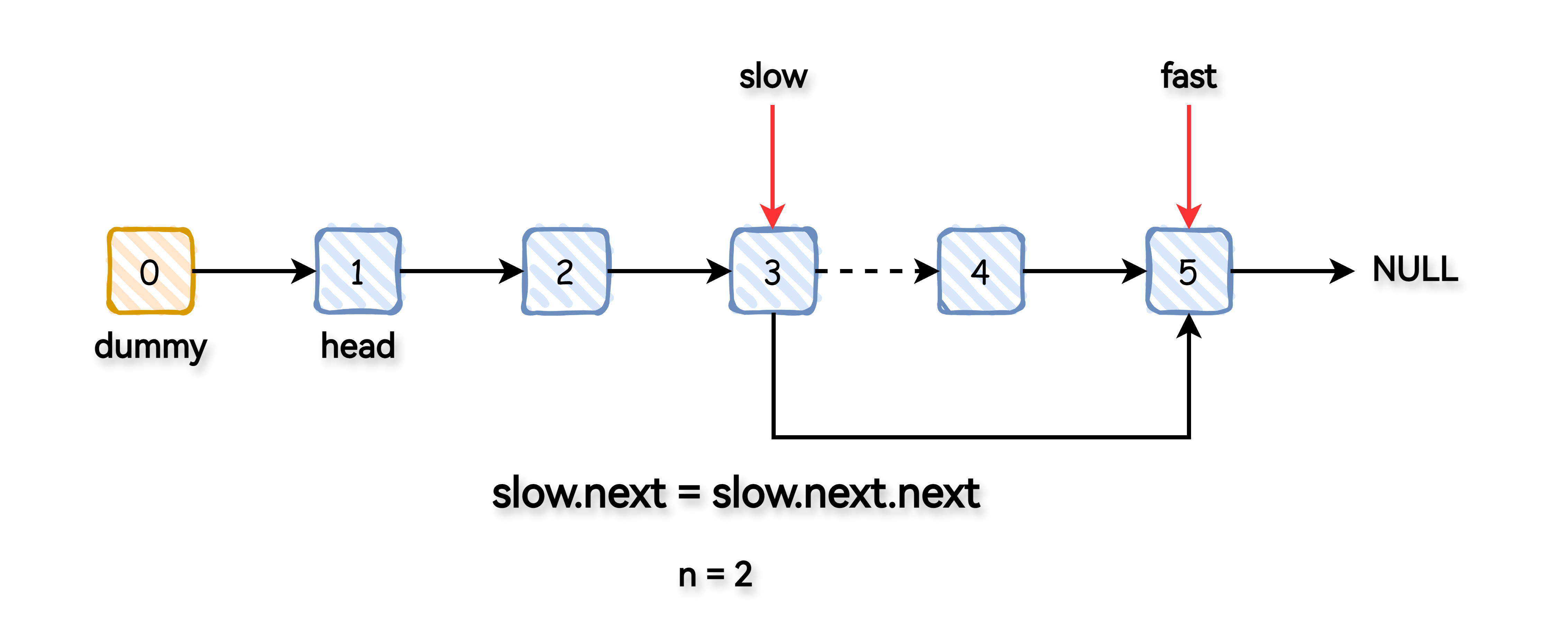
调整 slow 的 next 指针，跳过要删除的节点。

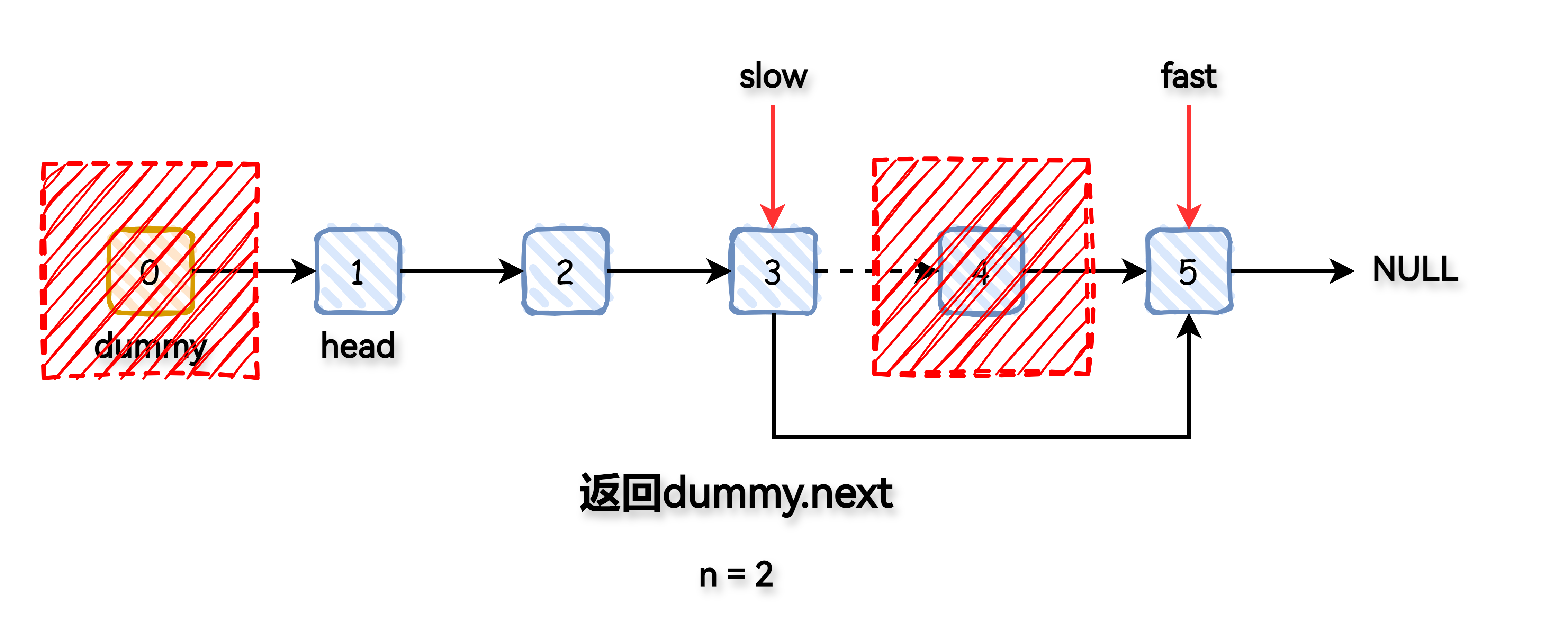
返回新的头节点 dummy.next。

代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
        # 创建哑结点并指向头结点
        dummy = ListNode(0, head)
        fast = dummy
        slow = dummy

        # 将 fast 指针向前移动 n 步
        for _ in range(n):
            fast = fast.next
        
        # 同时移动 fast 和 slow，直到 fast 到达链表末尾
        while fast.next:
            fast = fast.next
            slow = slow.next

        # slow 指向要删除节点的前一个节点，跳过要删除的节点
        slow.next = slow.next.next

        # 返回哑结点的 next，作为新的头节点
        return dummy.next

复杂度分析

时间复杂度：$O(n)$

空间复杂度：$O(1)$

24. Swap Nodes in Pairs

原题链接

题目描述

Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list’s nodes (i.e., only nodes themselves may be changed.)

Example 1:

1 2	Input: head = [1,2,3,4] Output: [2,1,4,3]

Example 2:

1 2	Input: head = [] Output: []

Example 3:

1 2	Input: head = [1] Output: [1]

Constraints:

The number of nodes in the list is in the range [0, 100].
0 <= Node.val <= 100

解题方法

本题要求两两交换链表中的节点，并且不能够直接修改原有节点中的值。

迭代

具体步骤：

创建一个哑节点 dummy，它的 next 指向链表的头节点，方便返回可能交换之后的头节点。
初始化一个指针 current 指向 dummy 节点。
遍历链表，直到 current 后没有一对可以交换的节点：
first.next 指向 second.next。
second.next 指向 first。
current.next 指向 second。
current 移动到 first 的位置，处理剩余节点。
返回 dummy.next。

递归

递归交换每一对相邻节点，然后将交换后的子链表连接起来。

递归过程：

如果没有可以交换的一对节点，直接返回当前的头节点。
否则，处理链表的前两个节点，并递归地交换后续节点。

假设当前链表为 head -> next -> ...，我们将 head 和 next 交换。
然后递归地处理从 next.next 开始的子链表，并将其连接到 head 后面。

返回新的头节点 next，因为 next 和 head 位置已经交换。

解题方法

迭代

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # 哑节点
        dummy = ListNode(0, head)
        current = dummy
        # 存在下一对可被交换的节点
        while current.next and current.next.next:
            first = current.next
            second = current.next.next
            # 交换两节点
            first.next = second.next
            second.next = first
            current.next = second
            # 处理下一对
            current = first
        # 返回头节点
        return dummy.next

递归

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # 如果没有可交换的一对节点，则返回当前节点
        if not head or not head.next:
            return head

        # 需要交换的一对节点
        first = head
        second = head.next

        # 递归交换节点
        first.next = self.swapPairs(second.next)
        second.next = first

        # 返回新的头节点（起始第二个节点）
        return second

复杂度分析

方法	时间复杂度	空间复杂度
迭代	$O(n)$	$O(1)$
递归	$O(n)$	$O(n)$（递归调用栈深度）

25. Reverse Nodes in k-Group

原题链接

题目描述

Given the head of a linked list, reverse the nodes of the list k at a time, and return the modified list.

k is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of k then left-out nodes, in the end, should remain as it is.

You may not alter the values in the list’s nodes, only nodes themselves may be changed.

Example 1:

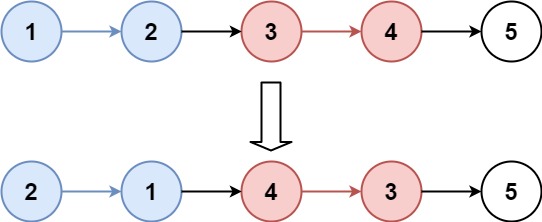
1 2	Input: head = [1,2,3,4,5], k = 2 Output: [2,1,4,3,5]

Example 2:

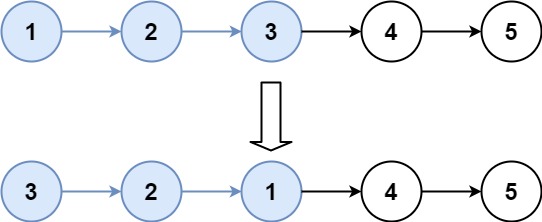
1 2	Input: head = [1,2,3,4,5], k = 3 Output: [3,2,1,4,5]

Constraints:

The number of nodes in the list is n.
1 <= k <= n <= 5000
0 <= Node.val <= 1000

Follow-up: Can you solve the problem in O(1) extra memory space?

解题方法

本题与上题两两一组反转链表有类似之处，是上一题的扩展版。思路也大同小异。

双指针

首先计算链表的长度，遍历一遍链表以获取其长度 n。

翻转每 k 个节点，以 k 为一组，使用两个指针，一个指针 prev 指向翻转组的前一个节点，要确保在翻转组的节点之前有足够的节点。翻转之后需要保持对翻转后的头节点与尾节点的引用。

将翻转后的组连接到链表中前面的部分和后面的部分，如果最后剩余的节点数量少于 k，则保持它们的原有顺序。

递归

递归地翻转每 k 个节点，并在每次递归结束后连接翻转后的部分。具体步骤如下：

递归终止条件：如果当前节点为 None 或剩余节点数少于 k，则返回当前节点。
翻转当前 k 个节点：在每次递归中，翻转当前的 k 个节点，并保持对头节点和尾节点的引用。
递归翻转后续节点：在翻转完成后，将当前组的尾节点连接到后续翻转后的头节点。
返回新的头节点：递归返回时，每层都返回翻转后的头节点。

代码实现

双指针

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
        # 统计链表长度
        length = 0
        count_node = head
        while count_node:
            length += 1
            count_node = count_node.next
        
        # 虚拟头节点
        dummy = ListNode(0, head)
        # 上一组结束的位置
        prev_group_end = dummy

        # 每 k 个为一组进行反转
        while length >= k:
            # 当前节点
            curr = prev_group_end.next
            # 下一组开始的位置
            next_group_start = curr
            
            # 开始反转
            prev = None
            for _ in range(k):
                next_node = curr.next
                curr.next = prev
                prev = curr
                curr = next_node
            
            # 拼接反转后的组
            prev_group_end.next = prev
            next_group_start.next = curr

            # 更新 prev_group_end 为当前组的末尾
            prev_group_end = next_group_start

            # 完成一组后减去 k
            length -= k

        return dummy.next

递归

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
        # 辅助函数，用于翻转链表的一个部分
        def reverseLinkedList(start, end):
            prev = None  # prev 指针初始化为 None
            current = start  # current 从 start 开始翻转
            while current != end:  # 当 current 不等于 end 时继续翻转
                next_node = current.next  # 记录当前节点的下一个节点
                current.next = prev  # 反转当前节点的指向
                prev = current  # 移动 prev 指针
                current = next_node  # 移动 current 指针到下一个节点
            return prev  # 返回翻转后的新头节点

        count = 0  # 计数器，用于计数节点
        node = head  # 从头节点开始遍历
        # 检查链表中是否有 k 个节点
        while node and count < k:
            node = node.next  # 移动到下一个节点
            count += 1  # 增加计数

        # 如果有 k 个节点可以翻转
        if count == k:
            reversed_head = reverseLinkedList(head, node)  # 翻转 k 个节点
            head.next = self.reverseKGroup(node, k)  # 递归翻转后续部分
            return reversed_head  # 返回翻转后的新头节点
        
        return head  # 如果不足 k 个节点，返回原头节点

复杂度分析

方法	时间复杂度	空间复杂度
双指针	$O(n)$	$O(1)$
递归	$O(n)$	$O(n)$（递归调用栈深度）

138. Copy List with Random Pointer

原题链接

题目描述

A linked list of length n is given such that each node contains an additional random pointer, which could point to any node in the list, or null.

Construct a deep copy of the list. The deep copy should consist of exactly n brand new nodes, where each new node has its value set to the value of its corresponding original node. Both the next and random pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list .

For example, if there are two nodes X and Y in the original list, where X.random --> Y, then for the corresponding two nodes x and y in the copied list, x.random --> y.

Return the head of the copied linked list.

The linked list is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:

val: an integer representing Node.val
random_index: the index of the node (range from 0 to n-1) that the random pointer points to, or null if it does not point to any node.

Your code will only be given the head of the original linked list.

Example 1:

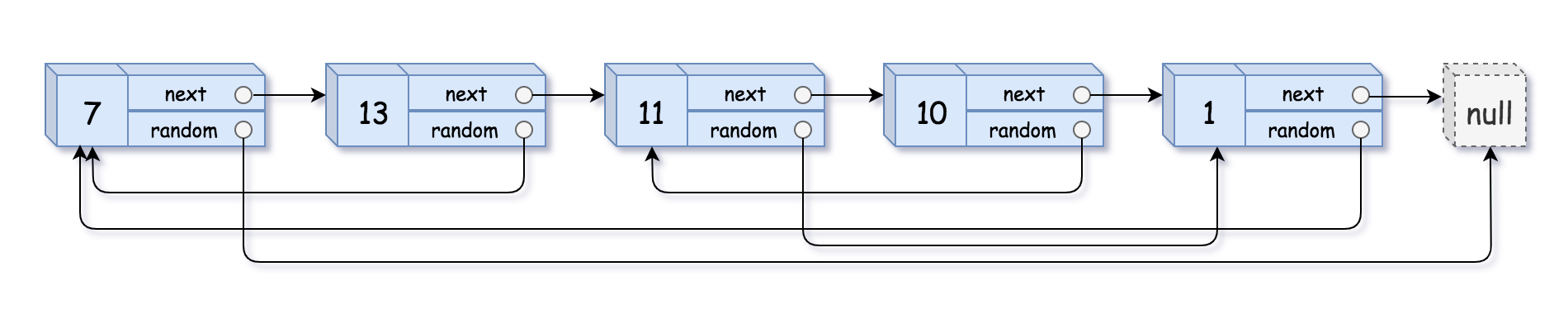
1 2	Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]] Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]

Example 2:

1 2	Input: head = [[1,1],[2,1]] Output: [[1,1],[2,1]]

Example 3:

1 2	Input: head = [[3,null],[3,0],[3,null]] Output: [[3,null],[3,0],[3,null]]

Constraints:

0 <= n <= 1000
-10^4 <= Node.val <= 10^4
Node.random is null or is pointing to some node in the linked list.

解题方法

该题目相当于对一个链表进行复制，麻烦的问题在于原链表中的每个节点包含一个随机指针 random，所以在构造新链表时需要考虑如何保证原链表中的随机指针的正确性。

迭代

遍历原链表，通过在每个原链表的节点之后复制一个相同的节点，之后再将随机指针补上，最后将新的链表从原链表分离出来也能够达到相同的效果。

创建新节点并插入到原链表的每个节点旁边：通过遍历链表，将每个节点的拷贝插入到它的下一个节点的位置，这样在链表中，原节点和对应的新节点是交替出现的。
复制 random 指针：由于新节点已经插入到了原链表的每个节点旁边，因此可以方便地通过原节点的 random指针找到对应的新节点的 random 指针。
分离链表：将交织在一起的链表分为两个链表，分别是原链表和新拷贝的链表。

哈希表

使用哈希表存储原链表的节点映射关系，之后根据哈希表构造新的链表。

步骤如下：

创建哈希表：使用一个字典来存储原节点与新节点之间的映射关系。
遍历链表：在第一次遍历中，为每个节点创建一个新节点并将其存入哈希表。
设置指针：在第二次遍历中，使用哈希表来设置每个新节点的 next 和 random 指针。

代码实现

迭代

"""
# Definition for a Node.
class Node:
    def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
        self.val = int(x)
        self.next = next
        self.random = random
"""

class Solution:
    def copyRandomList(self, head: 'Optional[Node]') -> 'Optional[Node]':
        if not head:
            return None

        # 第一步：在每个节点后面创建一个新节点
        cur = head
        while cur:
            new_node = Node(cur.val)
            new_node.next = cur.next
            cur.next = new_node
            cur = new_node.next

        # 第二步：复制 random 指针
        cur = head
        while cur:
            if cur.random:
                cur.next.random = cur.random.next
            cur = cur.next.next

        # 第三步：将新旧链表分离
        cur = head
        new_head = head.next
        new_cur = new_head
        while cur:
            cur.next = cur.next.next
            if new_cur.next:
                new_cur.next = new_cur.next.next
            cur = cur.next
            new_cur = new_cur.next

        return new_head

哈希表

"""
# Definition for a Node.
class Node:
    def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
        self.val = int(x)
        self.next = next
        self.random = random
"""

class Solution:
    def copyRandomList(self, head: 'Optional[Node]') -> 'Optional[Node]':
        if not head:
            return None

        # 创建哈希表
        old_to_new = {}

        # 第一步：复制节点并填充哈希表
        cur = head
        while cur:
            old_to_new[cur] = Node(cur.val)
            cur = cur.next

        # 第二步：设置 next 和 random 指针
        cur = head
        while cur:
            if cur.next:
                old_to_new[cur].next = old_to_new[cur.next]
            if cur.random:
                old_to_new[cur].random = old_to_new[cur.random]
            cur = cur.next

        return old_to_new[head]

复杂度分析

方法	时间复杂度	空间复杂度
迭代	$O(n)$	$O(1)$
哈希表	$O(n)$	$O(n)$

148. Sort List

原题链接

题目描述

Given the head of a linked list, return the list after sorting it in ascending order .

Example 1:

1 2	Input: head = [4,2,1,3] Output: [1,2,3,4]

Example 2:

1 2	Input: head = [-1,5,3,4,0] Output: [-1,0,3,4,5]

Example 3:

1 2	Input: head = [] Output: []

Constraints:

The number of nodes in the list is in the range [0, 5 * 10^4].
-10^5 <= Node.val <= 10^5

Follow up: Can you sort the linked list in O(n logn) time and O(1) memory (i.e. constant space)?

解题方法

解决这个问题的关键在于，我们需要对链表进行排序，同时要考虑时间复杂度和空间复杂度的要求。

题目要求我们将链表排序为升序，且在考虑 $O(n log n)$ 时间复杂度的情况下，比较适合的排序算法是 归并排序（Merge Sort），它可以在链表结构上实现 $O(n log n)$ 的时间复杂度。此外，归并排序可以在链表上进行原地排序，空间复杂度为 $O(1)$。

解决思路：

递归地拆分链表：
- 我们使用快慢指针来找到链表的中点。快指针每次走两步，慢指针每次走一步，当快指针到达末尾时，慢指针就位于链表的中点。
- 将链表从中点断开，形成两个子链表。
对两个子链表分别进行排序：
- 对两个子链表递归地应用归并排序。
合并两个排序后的子链表：
- 使用双指针技术将两个排序后的子链表合并成一个有序链表。

代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if not head or not head.next:
            return head
        
        # 找到中点
        def getMiddle(node):
            slow = node
            fast = node
            while fast.next and fast.next.next:
                slow = slow.next
                fast = fast.next.next
            return slow

        # 合并两个有序链表
        def merge(left, right):
            if not left:
                return right
            if not right:
                return left
            if left.val < right.val:
                left.next = merge(left.next, right)
                return left
            else:
                right.next = merge(left, right.next)
                return right

        mid = getMiddle(head)
        nextToMid = mid.next
        mid.next = None  # 将链表拆分为两个部分

        left = self.sortList(head)      # 排序左半部分
        right = self.sortList(nextToMid)  # 排序右半部分

        return merge(left, right)  # 合并两个已排序链表

复杂度分析

时间复杂度：$O(nlogn)$

空间复杂度：$O(logn)$

23. Merge k Sorted Lists

原题链接

题目描述

You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.

Merge all the linked-lists into one sorted linked-list and return it.

Example 1:

Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
  1->4->5,
  1->3->4,
  2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6

Example 2:

1 2	Input: lists = [] Output: []

Example 3:

1 2	Input: lists = [[]] Output: []

Constraints:

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] is sorted in ascending order .
The sum of lists[i].length will not exceed 10^4.

解题方法

考虑使用最小堆的做法，首先将每个链表的第一个节点加入最小堆，之后从堆中取出最小的节点，接着将该节点的下一个节点再次加入堆中，可以保证每次取出的节点都是当前所有链表中最小的。

而题目中给出的 ListNode 并不支持直接比较大小，你可以自定义比较函数或者用一个元组来确认如何在堆中进行大小的比较。

元组结构为 (node.val, i, node)：

node.val：节点的值，作为堆排序的依据，因为要求最后合并的链表是升序的，需要堆中始终保持最小的节点在顶部。
i：当前链表的索引（给链表编号），用于保证多个链表的节点值相同时能够保证顺序。
node：链表节点的实际对象。

代码实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        # 创建一个最小堆
        heap = []
        
        # 将每个链表的第一个节点加入堆中
        for i in range(len(lists)):
            if lists[i]:
                heapq.heappush(heap, (lists[i].val, i, lists[i]))

        dummy = ListNode()  # 哑节点，便于处理
        curr = dummy

        # 从堆中弹出最小的元素，然后将其后继节点再加入堆中
        while heap:
            val, idx, node = heapq.heappop(heap)
            curr.next = node
            curr = curr.next
            if node.next:
                heapq.heappush(heap, (node.next.val, idx, node.next))

        return dummy.next

复杂度分析

时间复杂度：$O(nlogk)$，其中 $k$ 为 $lists$ 的长度，$n$ 为所有链表的节点数之和。

空间复杂度：$O(k)$，堆中至多有 $k$ 个元素。

146. LRU Cache

原题链接

题目描述

Design a data structure that follows the constraints of a Least Recently Used (LRU) cache .

Implement the LRUCache class:

LRUCache(int capacity) Initialize the LRU cache with positive size capacity.
int get(int key) Return the value of the key if the key exists, otherwise return -1.
void put(int key, int value) Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.

The functions get and put must each run in O(1) average time complexity.

Example 1:

Input
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
Output
[null, null, null, 1, null, -1, null, -1, 3, 4]

Explanation
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1);    // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2);    // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1);    // return -1 (not found)
lRUCache.get(3);    // return 3
lRUCache.get(4);    // return 4

Constraints:

1 <= capacity <= 3000
0 <= key <= 10^4
0 <= value <= 10^5
At most 2 * 10^5 calls will be made to get and put.

解题方法

要设计一个满足 LRU (Least Recently Used) 缓存约束的数据结构，可以使用一个哈希表（dict）加上一个双向链表来实现。

设计思路

哈希表 (dict):
- 用来存储缓存的键值对，以便在 O(1) 时间复杂度内访问缓存中的数据。
- 键是缓存的 key，值是双向链表中对应节点的指针。
双向链表:
- 用来维护元素的访问顺序，最近使用的元素放在链表的头部，最久未使用的元素放在链表的尾部。
- 通过双向链表，我们可以在 O(1) 时间复杂度内将某个元素移动到链表头部，以及在缓存容量超出时删除尾部的元素。

操作流程

get(key):
- 如果键存在于缓存中，从哈希表中获取该键对应的链表节点，并将该节点移动到链表的头部（因为这是最近被访问的）。
- 如果键不存在，返回 -1。
put(key, value):
- 如果键已经存在，更新对应的值，并将该节点移动到链表头部。
- 如果键不存在，创建一个新的节点，插入到链表头部，并更新哈希表。
- 如果插入后缓存的大小超过了容量限制，需要移除链表尾部的节点，同时在哈希表中删除对应的键。

代码实现

class Node:
    def __init__(self, key=0, value=0):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None

class LRUCache:

    def __init__(self, capacity: int):
        self.capacity = capacity
        self.cache = {}  # 存储键与节点的映射
        self.head = Node()  # 虚拟头节点
        self.head.next = self.head.prev = self.head  # 初始化为环形

    def _remove(self, node: Node):
        """从链表中移除节点"""
        node.prev.next = node.next
        node.next.prev = node.prev

    def _add_to_head(self, node: Node):
        """将节点添加到链表头部"""
        node.next = self.head.next
        node.prev = self.head
        self.head.next.prev = node
        self.head.next = node

    def get(self, key: int) -> int:
        """获取键对应的值"""
        if key in self.cache:
            node = self.cache[key]
            self._remove(node)  # 移除节点
            self._add_to_head(node)  # 重新添加到头部
            return node.value
        return -1

    def put(self, key: int, value: int) -> None:
        """添加或更新键值对"""
        if key in self.cache:
            node = self.cache[key]
            self._remove(node)  # 移除旧节点
            node.value = value  # 更新值
            self._add_to_head(node)  # 重新添加到头部
        else:
            if len(self.cache) >= self.capacity:
                # 超过容量，移除最少最近使用的节点
                lru = self.head.prev
                self._remove(lru)
                del self.cache[lru.key]  # 从哈希表中删除
            new_node = Node(key, value)
            self.cache[key] = new_node  # 添加到哈希表
            self._add_to_head(new_node)  # 添加到链表头部


# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

复杂度分析

无，这是模拟